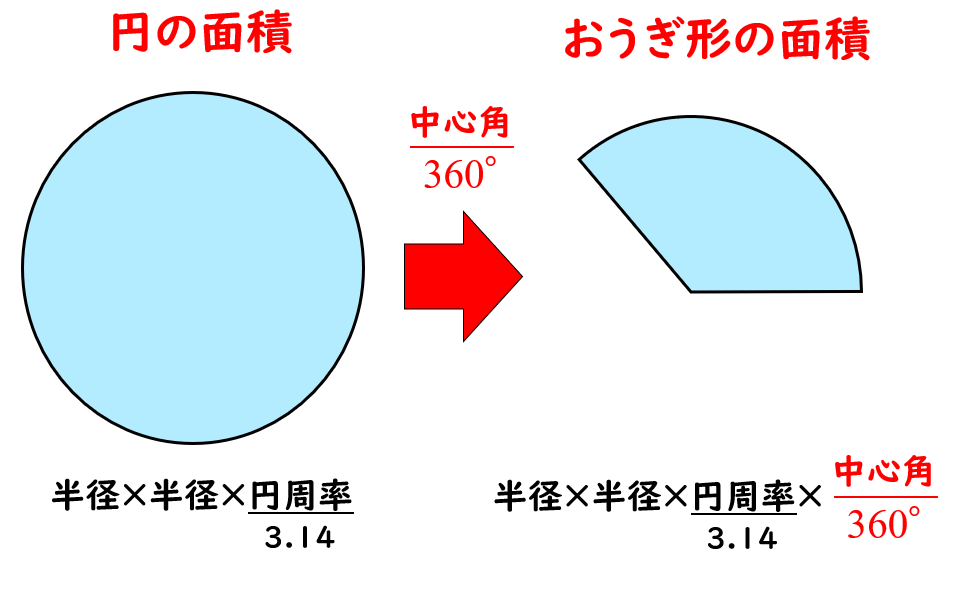
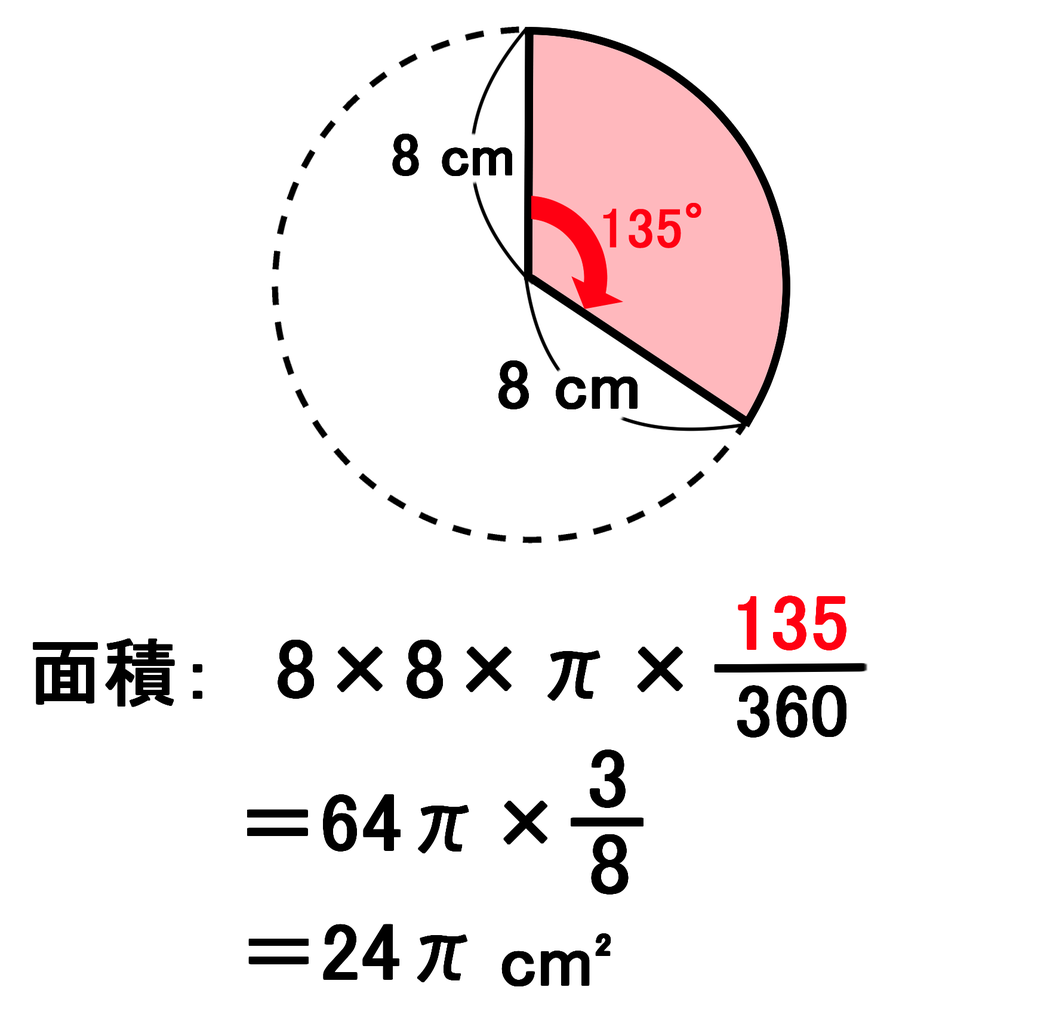
おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と比べた時にどれくらいの割合なのか ということ。 たとえば中心角が 270° 270 ° 、 180° 180 ° 、 90° 90 ° 、 45° 45 ° といったおうぎ形は元の円と比べるとそれぞれ 3 4 3 4 、 1 2 1 2 、 1 4 1 4 、 1 8 1 8 の大きさになっているのは明らか 扇形の中心角の求め方の公式を知りたい! こんにちは、この記事をかいているKenだよー!豆乳ラテだったら3杯はいけるね。 「扇形の中心角の求め方」の公式 ってチョー便利。 教科書にはのっていない「知る人ぞ知る公式」なんだ。楕円の2つの角度に挟まれる扇形の面積と楕円弧の長さを計算します。 角度 θ 0 度 ラジアン;
おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun
扇形 面積 求め方 小学生
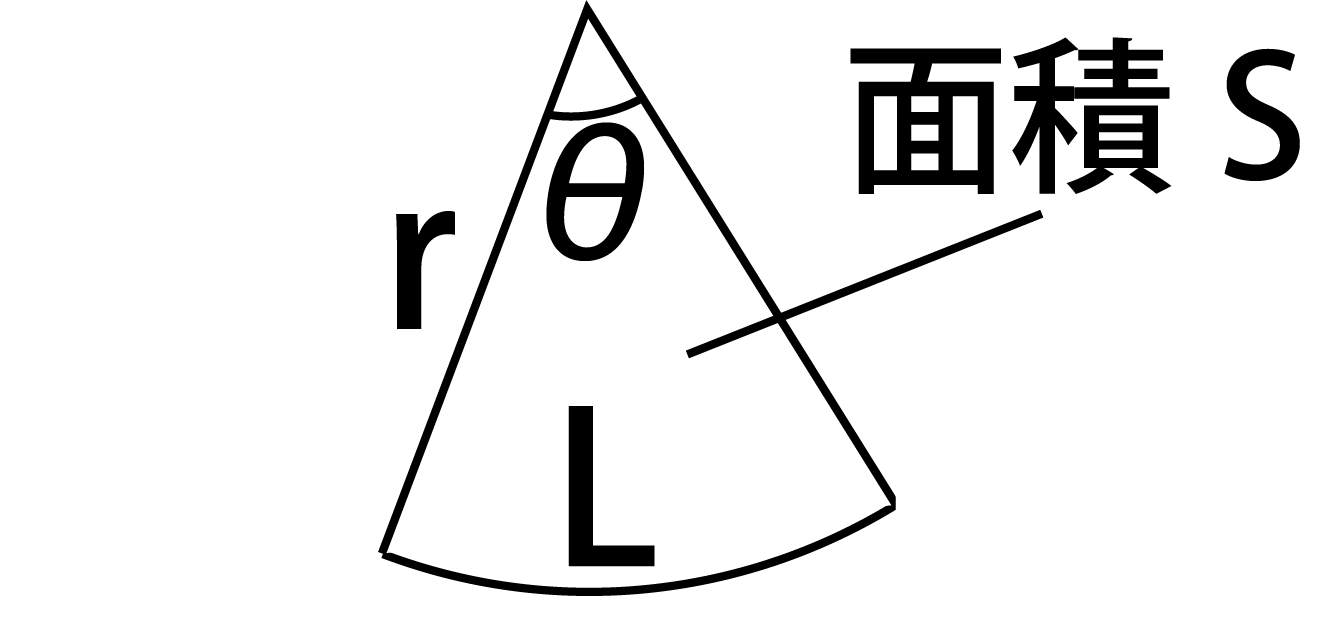
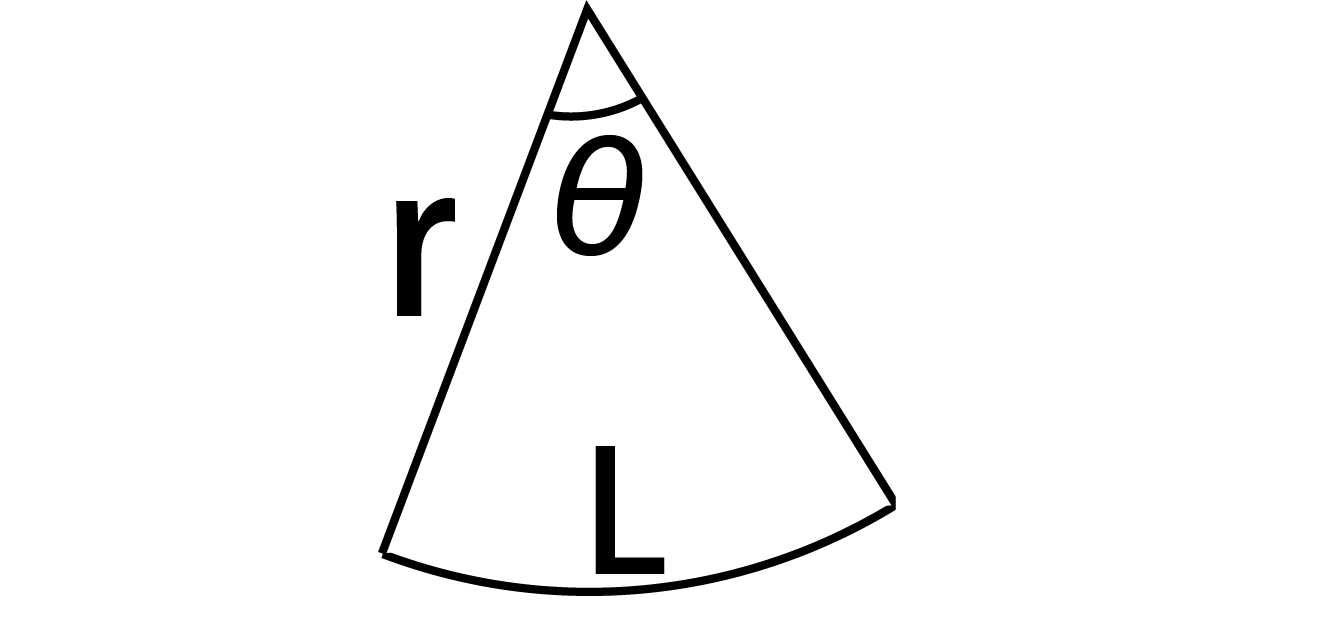
扇形 面積 求め方 小学生- coo******** さん 13/7/16 1731(編集あり) >簡単な扇形の中心角の求め方を教えてください 何から求めるかにもよります。 半径と弧の長さから求めるのであれば、 中心角=弧の長さ÷(半径×2π)×360° 半径と扇形の面積から求めるのであれば、 中心角=面積÷(半径×半径×π)×360° など。 >円錐の表面積で中心角を普通に解くときは円周×a/360が多い まず面積の求め方 扇形 扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。 また、2行目の l は扇形の弧の長さを表します。 このページの続きでは、この 公式の導き方 と、 扇形の面積を求める計算問題の解き方




扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト
三角形abcの辺abをaの方へabと同じだけ延ばした点をd、辺bcをbの方へbcの3倍だけ延ばした点をe、辺caをcの方へcaの2倍だけ延ばした点をfとします。三角形defの面積は三角形abcの面積の何倍ですか。 → 解答 問題4 たて5cm、よこ9cmの長方形の紙が4まい、図のように重なっています。ア、イ 正方形の面積=,10×10=100 (㎠) 100:面積=1:057 面積=57㎠ と求めることができる。 円周率が314の時しか使えません。 公式として覚えているだけでは、中学生になってから問題を解けなくなってしまいます。 基本的な考え方で求められるようになってから、公式として覚えていくようにしましょう。 扇形の面積の求め方は、半径と中心角から求める方法が一般的です。 半径と中心角から扇形の面積を求める 扇形の面積は、 半径 × 半径 × 円周率 × θ / 360 で求めることができます。 半径rの円の面積の θ / 360 倍の大きさで求める方法です。 頭の中に
小学6年生の算数 円の面積 問題プリント ツイート; フォローをありがとうございます。 扇形は、円を分割してできた形なので、半径はどこも同じです。 なので、大きい扇形の半径は小さい扇形の半径と書いてある3センチを合わせて6センチとなります。 なので、大きい扇形の面積から、小さい扇形の面積を引いたものが、求めたい面積です。 側面である扇形の面積を求めようとすると、扇形の公式から分かるように 中心角が必要になります。 というわけで、 まずは扇形の中心角を求めていきます。 底面の円周の長さと側面の弧の長さが等しいことを利用すると
これらの情報を元に、扇形の表面積を求めて生きたいと思います。 扇形の面積 = 底面の円の面積 + 扇形の面積 = r × r × π + ( l × l × π ) × 2rπ / 2lπ = r 2 π + lrπ これで、扇形の表面積を計算することができました。毎回このように計算してももちろんよいのですが、この計算結果から1つ 円錐の表面積の求め方がわかる3ステップ 円錐の表面積は3ステップで計算できちゃう^_^ つぎの例題をときながらみてみよう。 半径3cm、母線の長さが10cmの円錐の表面積を10秒以内に計算して。 Step1 底面の「円周の長さ」を計算したる まずは底面の「円周角度 θ 1 θ 0 と同じ単位;



扇形 面積の計算 計算サイト




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
面積=(一辺)×(一辺)×043 正三角形とは、三角形の全ての辺の長さが等しい三角形のことをいいます。 こちらも三角形なので、「底辺×高さ÷2」で求められます。 高さが分かっている場合は、この公式で問題無いですが、高さが分かっていない場合は、一辺×一辺×√3÷4という公式になります。 しかし小学生では、まだ√(ルート)を指導しないため、√3÷4を 扇形の面積の求め方 公式と計算例 円 扇形 の面積 周や弧の長さの公式 数学fun 中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学 カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 中学受 ★扇形の中心角の求め方★途中式をていねいに解説!面積、弧の長さから求める方法 kaztaro ゆい 扇形の中心角を求めれるようになりたいですっ!! かず先生 よし! それじゃぁ、扇形の中心角について学んでいこう! 今回の記事では扇形の中心角を求める方法について解説していきま




なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア
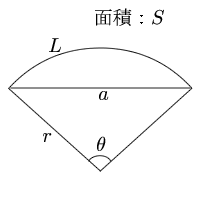
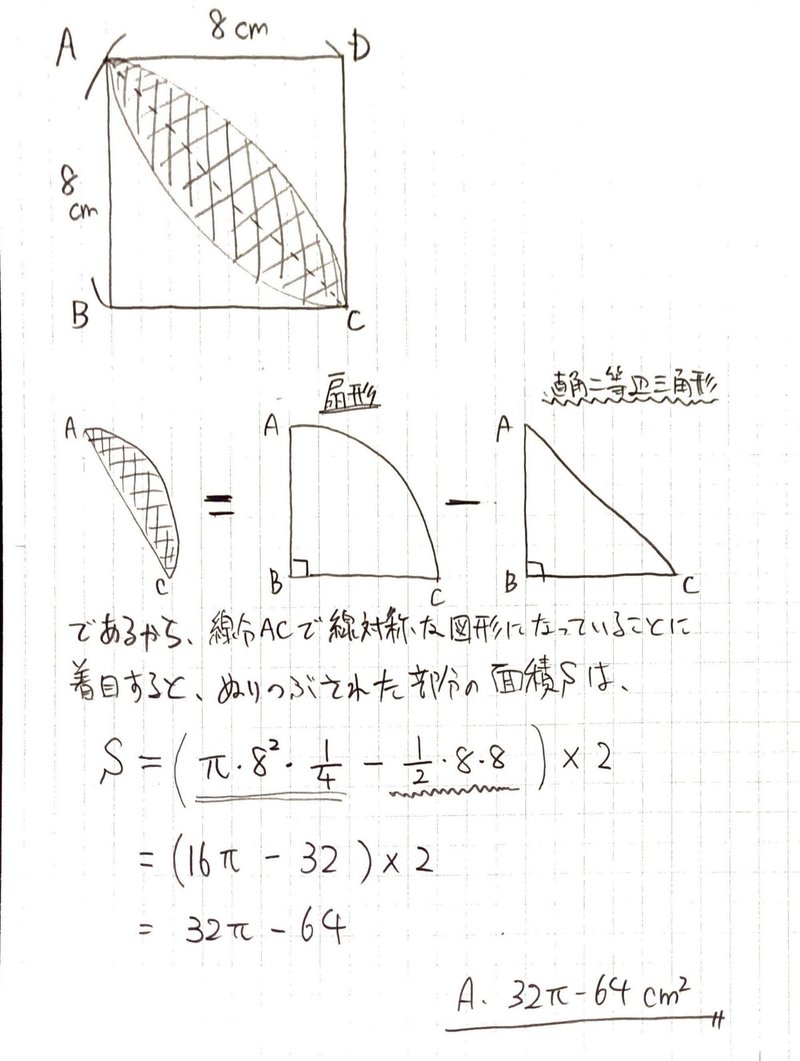
扇形(おうぎ形)の面積の求め方 小6 算数「面積」1 組 番 氏名 千葉県 小6 算数「面積」1 解答・解説 (1)図1で,色をぬってある部分の面積を求めましょう。また,面積の求め方を説明し ましょう。(解答) 912 2 (説明) その1 半径が4 の 円2つの面積の和は,1辺4 の正方形よりも色面積 S 円弧の長さ L 弦の長さ c お客様の声 アンケート投稿 よくある質問 リンク方法 扇形の面積 110 /26件 表示件数 1 0852 30 木の葉形面積の求め方は?(滝中学 14年) 二番目に短いひもの長さは?(広島学院中学 14年) 色部分の面積は?(15年 学習院女子中等科) 色部分の面積は?(今年、16年 ラ




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト



子供に説明できる 円の面積の公式 の証明 Nikkei Style
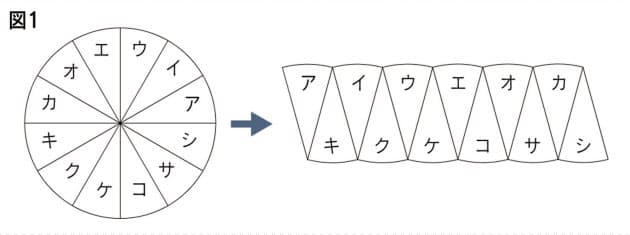
小学生の算数 図形・面積・体積 練習問題プリント 無料ダウンロード・印刷 ;求める面積は左図のχの部分 つまり、正方形から a,b,c,dの4カ所を ひいてやれば良いことが分かる! a,b,c,d は合同なので a の面積だけの求め方を考える! a の部分の面積を求めるには左図の手順でよい! (扇形の面積)=π(10) 2円の面積の求め方 (小学生の算数で習った方法、計算は高校生レベル) 08年08月09日1002 小学生の時、教科書に円の面積の公式が 半径×半径×円周率 πr^2 であることについて、もちろん積分したら終わりなんですが こうやって円を何等分かの扇形に分割し




裏技 おうぎ形の面積を一瞬で求める 弧の長さを利用した裏技公式 中学数学 平面図形 2 Youtube




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題
小学生の算数問題です扇形の面積を求めるのですが半径が10㎝、角度は60℃わか Yahoo!知恵袋 扇形の面積を求める公式は、 半径×半径× 円周率 ×角度 です。 よってこの問題は、 10×10×314×60÷360 という式になります。 年代によって円周率が3だったり314だったりするので、そこは学校で習った数値を入れてください。 円は360℃で、そのうちの60℃の面積を 円・扇形の公式まとめ 円周: 2πr 2 π r 円の面積: πr2 π r 2 扇形の弧の長さ: 2πr× a 360 2 π r × a 360 扇形の面積: πr2 × a 360 π r 2 × a 360 扇形の面積(弧の長さ l l からの導出): 1 2lr 1 2 l r ※半径: r r 、円周率: π π 、中心角: a a 、扇形の弧の長さスマートフォン 扇形の半径と中心角から扇形の面積、円弧の長さ、弦の長さを計算します。 半径 r 中心角 θ 度 ラジアン;



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋




ボード 復習 のピン
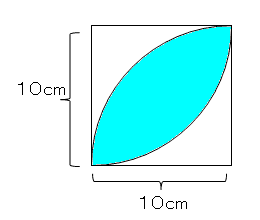
小学6年生の算数 角柱や円柱の体積の求め方・公式 問題プリント 小学6年生の算数角柱や円柱の体積の求め方・公式の練習問題プリントを無料ダウンロード・印刷 葉っぱ1枚分の面積を求めて4倍すれば、四つ葉の面積になります。 右の図のように、四つ葉を 分解 して考えると、葉っぱ1枚が入っている正方形の一辺の長さは、5cmです。 葉っぱ1枚分の面積は、葉っぱ公式により 5cm×5cm×057=1425cm² よって 四つ葉の面積は さらに、それぞれの円の扇形から三角形を引いたものを足せば赤色の面積が求められることが見えます。 図のように角度θ1、θ2を置くと、 s = ((円O1の角度θ1扇形の面積) (円O2の角度θ2扇形の面積) (三角形AO1O2の面積)) * 2 と求められます。それぞれについ




円錐の表面積の求め方 You Look Too Cool



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ
半径 a 半径 b 扇形の面積 S 楕円弧の長さ L 関連リンク 楕円の弧長の求め方 お客様の声 アンケート投稿 よくある質問 リンク方法 楕円扇形の面積 00 / 0件 表示件数 扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題 おうぎ形の面積の求め方 次世代型個別指導塾アチーブメント Achievement なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル 中1数学 おうぎ形の面積 弧の長さ 中心角の 《平行四辺形の面積の求め方》 平行四辺形の面積=底辺×高さであることから この平行四辺形の面積=67×45=3015(㎠) 答え 3015㎠ 問題③ 面積が108㎠である、次の平行四辺形の高さを求めましょう。 《平行四辺形の高さの求め方》 平行四辺形の面積=底辺×高さより この平行四辺
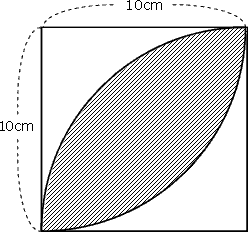



面積の求め方 算数の教え上手 学びの場 Com




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち
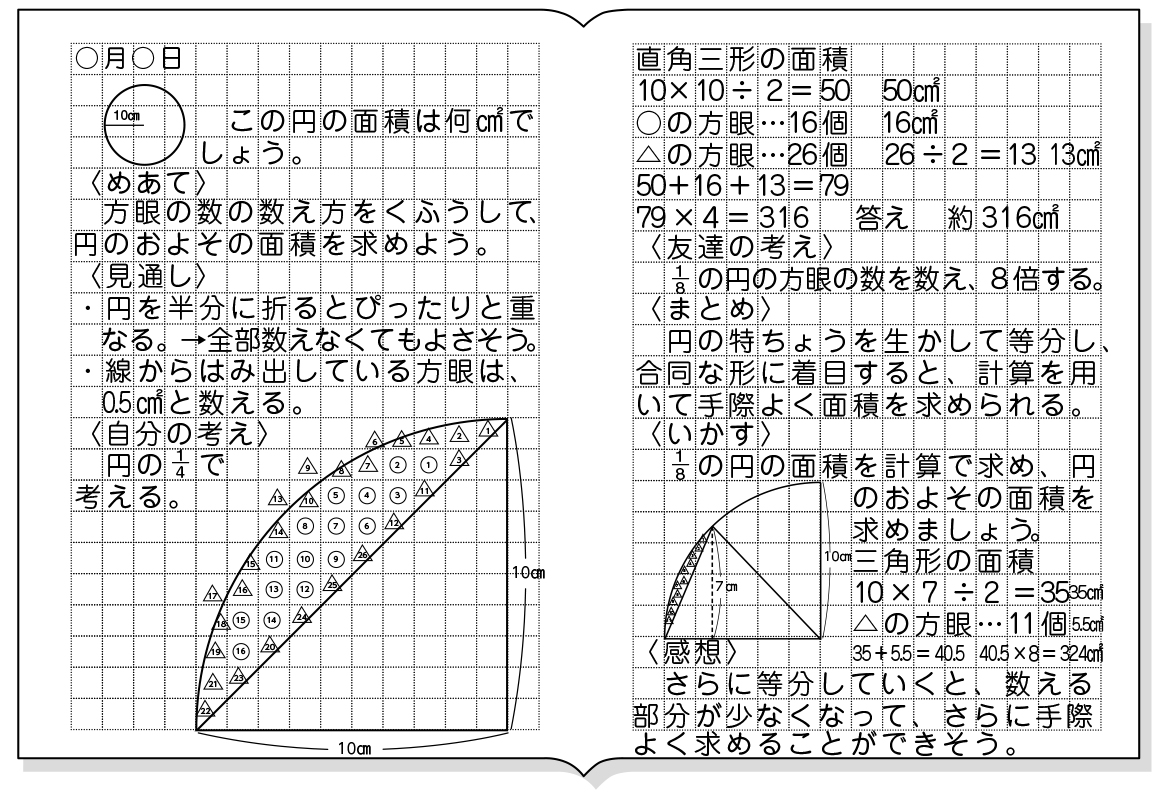



小6算数 円の面積 指導アイデア 1 みんなの教育技術




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素




円 扇形 の面積 周や弧の長さの公式 数学fun




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




扇形の中心角の求め方を教えてください Clearnote
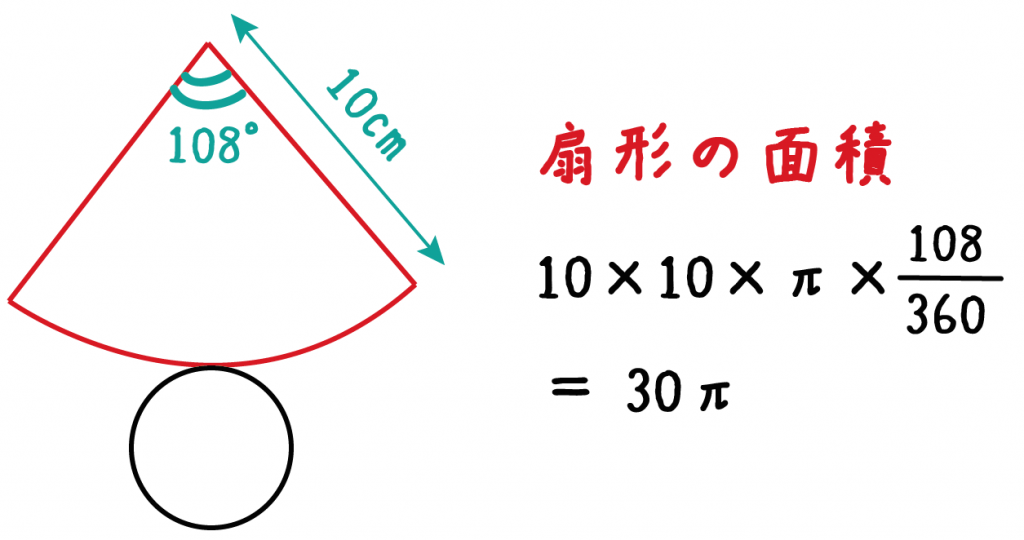



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
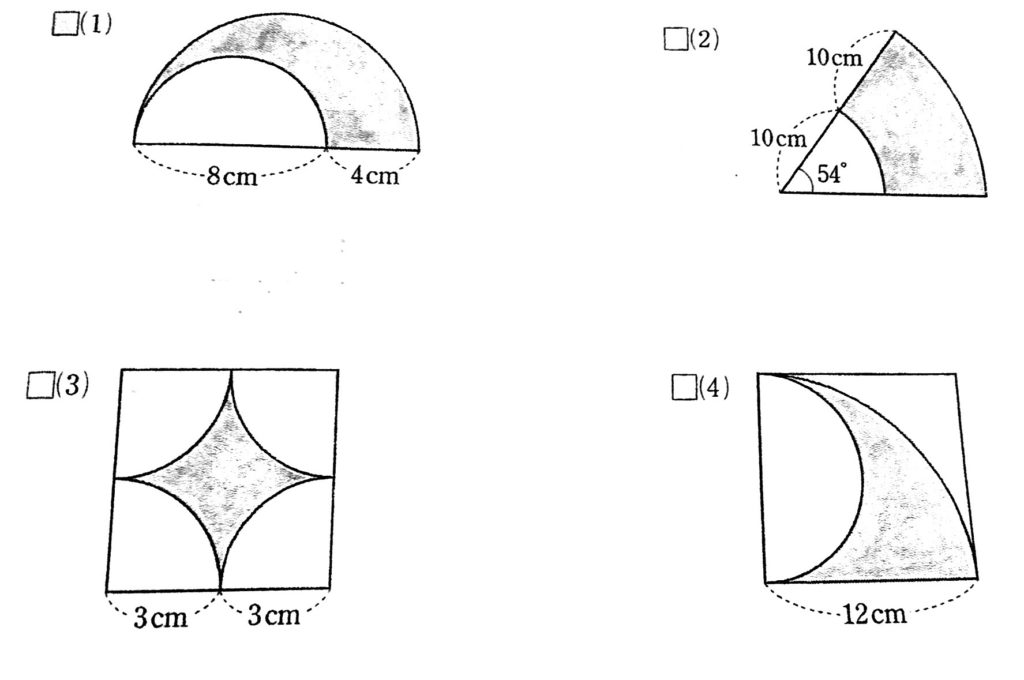



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




至急です 扇形の面積の公式を使って色がついている部分の面積を求めなさいという Clearnote
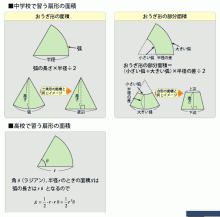



三角形と扇形の面積 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学



3




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題



扇形の中心角の求め方




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく
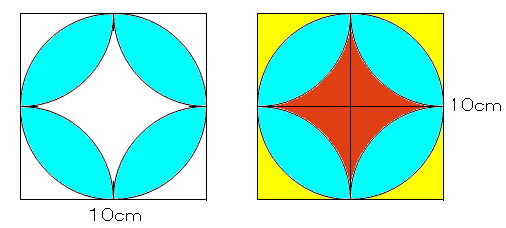



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素
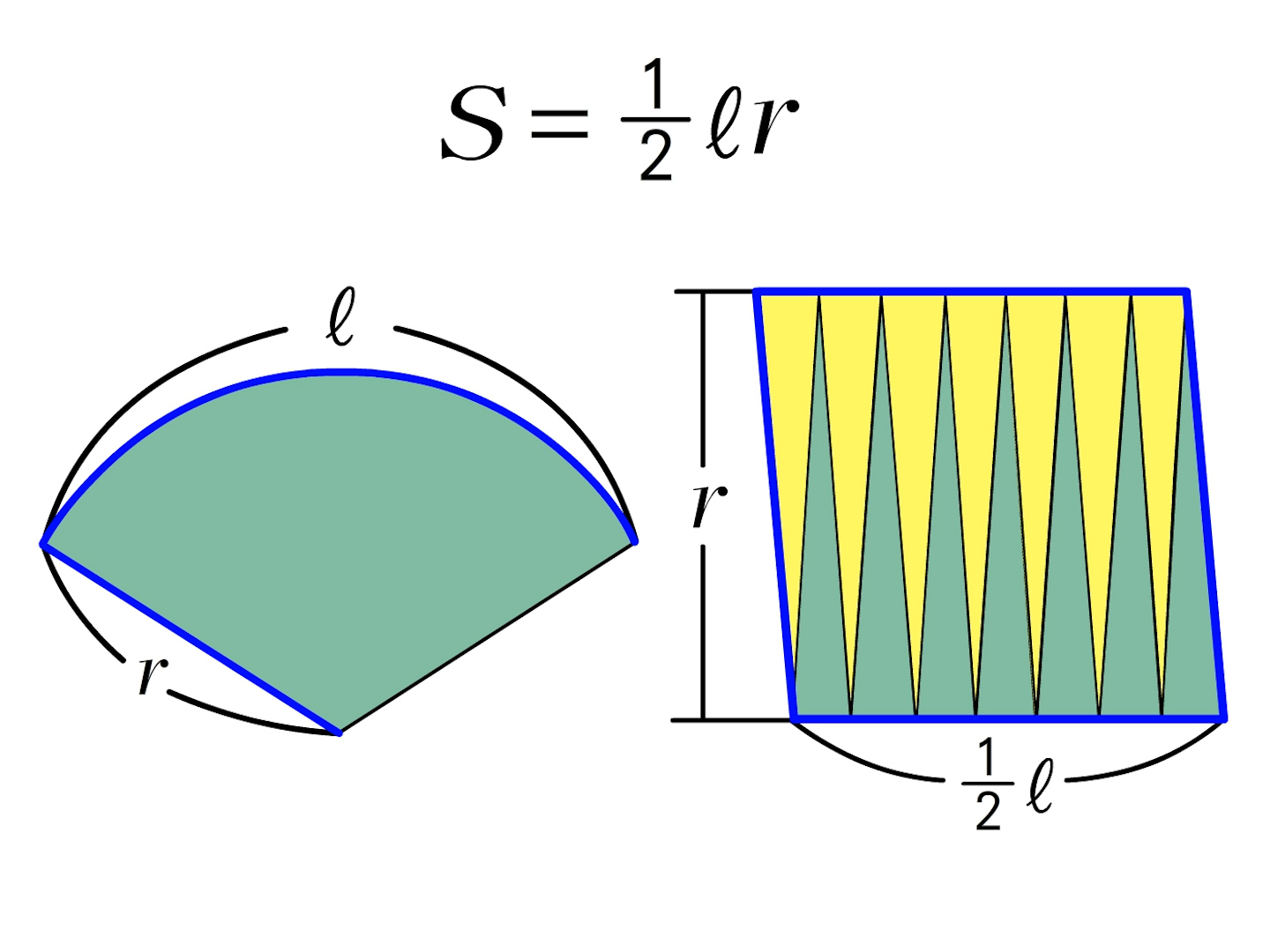



1年 おうぎ形の面積 数学イメージ動画集 大日本図書




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




タダ塾 小6算 円の面積5 連問2 Youtube




扇形の半径の求め方 計算のやり方をイチから解説していくぞ 中学数学 理科の学習まとめサイト



物理のための数学 図のbを含む扇形の面積の求め方を教えてくださいますでしょう Yahoo 知恵袋




円弧面積の計算式




扇 おうぎ 形の面積を求める公式と弧の長さの求め方




円 扇形 の面積 周や弧の長さの公式 数学fun




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円の面積 練習応用 Youtube




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか
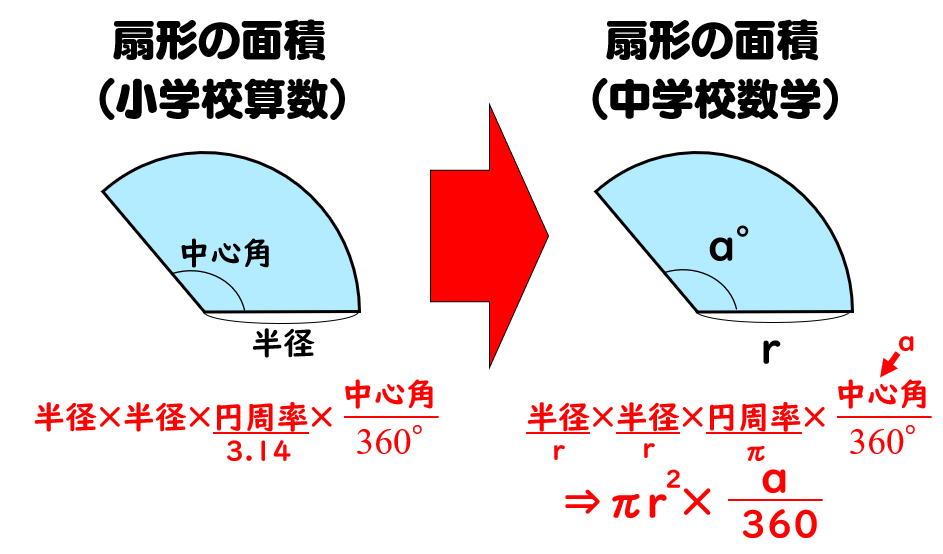



円 扇形 の面積 周や弧の長さの公式 数学fun




はっぱ型 の図形の面積 身勝手な主張



おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




小6 算数 小6 2 円の面積 応用編 Youtube




標準 おうぎ形と正方形の面積 なかけんの数学ノート




円の周りの長さを計算しよう 家庭学習レシピ




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clearnote



他の解き方ないんですか Katsuya Saito Note




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




扇形の面積の求め方 公式と計算例



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



1



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ



2




この図形の色を塗った部分の面積の求め方を教えてください この図形 小学校 教えて Goo




面積の求め方 算数の教え上手 学びの場 Com




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




おうぎ形の弧の さと 積の求め方 中学受験プロ講師ブログ




おうぎ形の面積の求め方2つと葉っぱ レンズ 形の面積の求め方3つ 等積移動 中学受験 塾なし の勉強法




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun



3




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張




円 扇形 の面積 周や弧の長さの公式 数学fun




扇形面積求め方 扇形の弧の長さと面積 小學 中學數學での平面図形の Txfs Co




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ




正方形扇形面積 扇 おうぎ 形の面積を求める公式と弧の長さの求め方翻譯此網頁 Voajcr




色のついた部分の面積の求め方を教えてください Clearnote




おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト




扇形の弧の長さの求め方 公式と計算例




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学
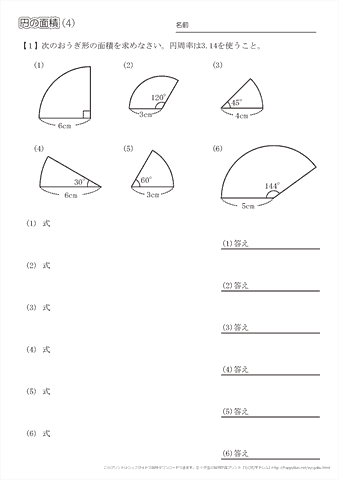



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト




扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー




扇形の面積の求め方 公式と計算例




扇形面積求め方 扇形の弧の長さと面積 小學 中學數學での平面図形の Txfs Co



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典



色のついた部分の面積を求めなさい ただし 円周率はpとします この問 Yahoo 知恵袋



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
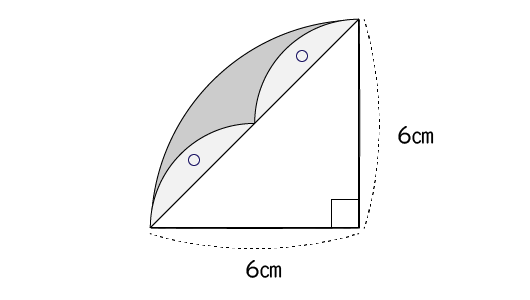



中学1年生数学 複雑な面積の求め方 長野地区 Itto個別指導学院 長野市の学習塾



0 件のコメント:
コメントを投稿