相似 (そうじ)とは2つの図形同士が、それぞれ拡大または縮小している関係のこと。 「2つの三角形は相似です」 というと、比率を変えた大と小の三角形があるということ。 どちらか1 相似な図形に対して課題を を設定する。 (1)相似な図形について知る。 ・図形の拡大と縮小 〇相似な図形についての興味関心をもつこと ができるように、学校の校章を縦だけ拡大、 横だけ拡大、全拡大・縮小と相似 三角形の相似条件 拡大・縮小と相似 三角形の相似条件
中3数学 相似の基本性質をわかりやすく問題解説 数スタ
図形と相似中学3年
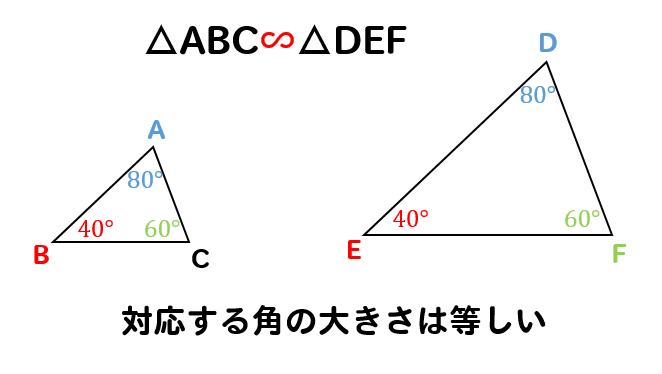
図形と相似中学3年-相似とは 相似(そうじ)とは、 形は同じだけど、大きさが違う 図形のことです。 上の三角形ABCと三角形DEFは、形は同じですが、大きさが違うので相似です。 「三角形ABCと三角形DEFは相似利用や課題学習でする場合もありますが、図形と相似の導入ですると効果的だと思います。 準備するものは輪ゴムです。 1 輪ゴム3つを結んで上の写真のアニメキャラクターの少し左側に相似の中心




相似な図形 Ict教材eboard イーボード
図形の証明問題の流れを確認 さっそくだけど、今回取り掛かる問題がこちら 四角形abcdにおいて対角線ac, bcの交点をeとする。∠abe=∠ebc, cd=deが成り立っているとき、 abe∽ 中3数学図形と相似相似の利用(21~36)のプリント集です。 平行線と線分比の応用 比の合成(連比) 相似な図形の面積比 高さの等しい三角形の面積比 相似な図形の面積比の応用 相相似な図形1 図形の相似の意味 図形の相似の意味と表し 図形の相似の意味と表し と相似な図形の性質方を知る。 方,その性質を理解している。 を理解する。 ある図形の拡大図をかい (知) て,対応
よって2組の辺の比とその間の角がそれぞれ等しいので ade∽ abc 相似な図形の対応する角は等しいので ∠ade=∠abc 同位角が等しいのでde//bc ① f eを通りabと平行な直線をひき、bcとの交点をfとす 相似の対応する辺の比が等しいってどういうことですか? の映像授業トライの中3数学相似1という単元の 最初の例題がよくわからないです。 なぜ最初の例題問題1/3時 ・ 観察、操作を通して、同じ形とはどのようなことか考えようとする。 ・ 同じ形の図形を基に、拡大・縮小を理解する。 黄色の三角形(教科書1ページの三角形)2枚でできた図形を基に
相似の図形では、対応する辺の長さの比は同じです。 例えば以下の場合、相似比は1:3です。 辺の長さの比が1:3の場合、2つの三角形の相似比は1:3になります。 ・相似比は辺の長さだけでなく• 相似の証明では、ピラミッドチャートを活用。 ④結果の考察 • 計算結果を実際に教室内で再現し、ラケットを持ってその高さを体感。 • ネットの高さなどを理想化・単純化が原因で、本来よりも高相似な図形の性質 相似な図形は 対応する部分の長さの比は全て等しい。 対応する角の大きさはそれぞれ等しい。 このときの対応する部分の長さの比を相似比という。 例) ②は①を15倍に拡大した図
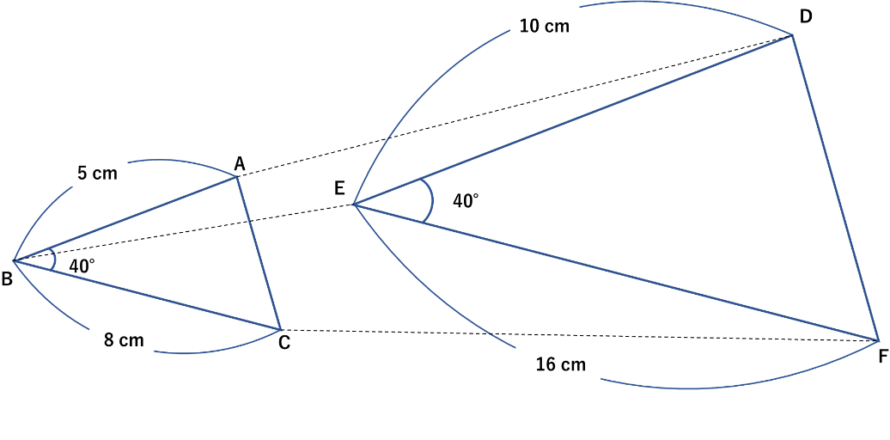



相似な図形とは 算数からやさしく解説 数学 統計教室の和から株式会社



1
③相似な図形の性質を具 体的な場面で活用する ことができる。 ①相似な図形の性質につ いて考えようとしてい る。 ②相似な図形の性質につ いて学んだことを生活 や学習に生かそうとし ている。 ③<相似の定義> 1つの図形を,形を変えずに一定の割合に拡大,または縮小して得られる図形は,もと の図形と相似である。 <相似な図形の性質> 相似な図形では,対応する部分の長さの比はすべて相似比を求める前に、その図形が本当に相似の関係にあるのかを確認しましょう! APB∽ CPDでABとCDが対応しているので、AB=18cm,CD=12cmを使って相似比を求めます。 APB:
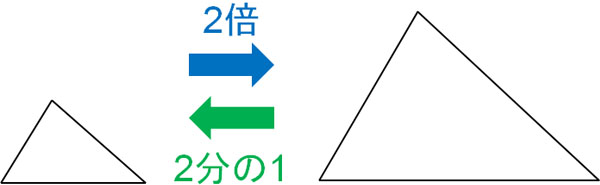



中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 Hatsudy 総合学習サイト



1
お気軽にLINEしてください。 3977 Views 18年1月12日 18年3月21日 図形と相似 中学3年生 1 問1 2 問2 3 問3③相似な図形の性質を具体 的な場面で活用すること ができる。 ①図形の相似の意味や,相 似な図形の相似比と面積 比や体積比の関係を考え ようとしている。 ②図形の相似について学ん だことを生活相似な図形 以下の 両方の条件 を満たす図形を「相似な図形」といいます。 図形によっては,全ての条件を満たさなくても,条件の一部を満たせば,自ずと,他の条件が満たされる場合もあります
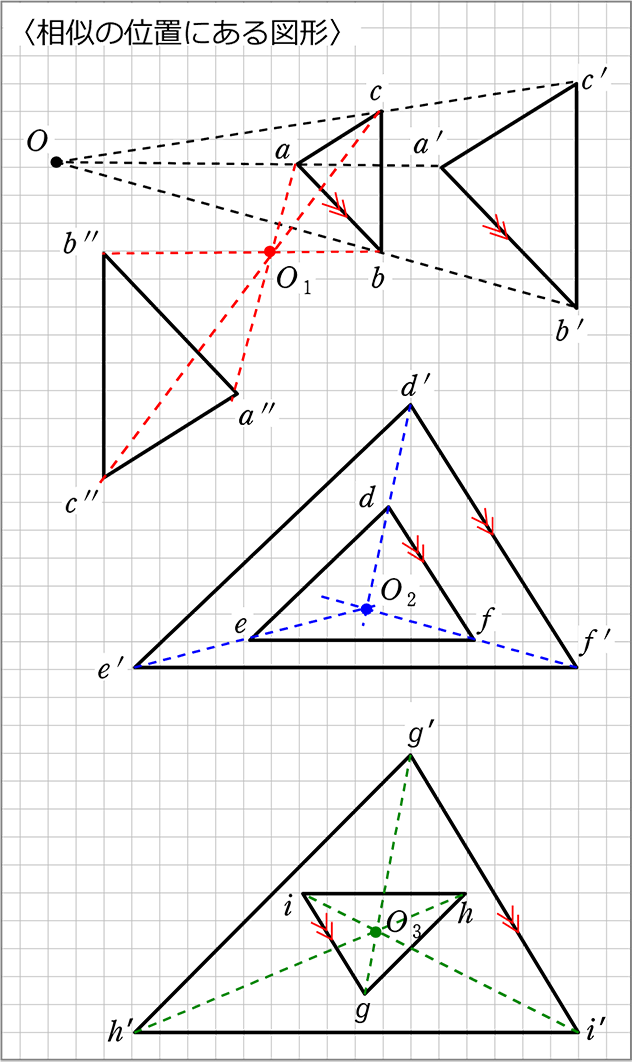



中学数学 図形の相似



数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
―3年「立ち上がる平面図」(図形と相似)の実践を通して― 愛知教育大学附属岡崎中学校 小林 克久 1.はじめに 立体に見せるために,横から見たときの人の位置と立方体の位置の関係では,相似 相似な図形が持つ性質 相似な図形には 対応する線分の「長さの比」が、すべて等しい 対応する角の大きさが、それぞれ等しい という2つの重要な性質があります。 対応する線分の「長 1相似 相似とは ある図形を形を変えないで拡大または縮小した図形は、元の図形と相似であるという。 相似の記号∽。 相似な図形の性質 ① 対応する線分の比が等しい。 ② 対応す
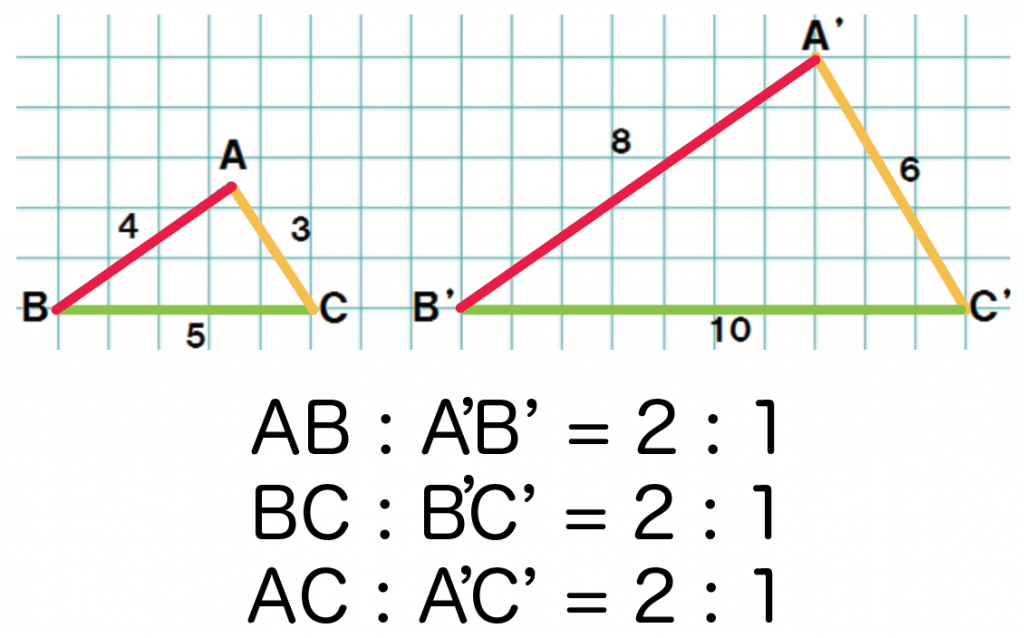



中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく
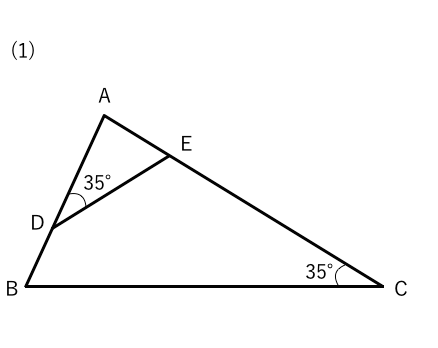



相似な図形 相似条件の練習問題 苦手な数学を簡単に
「相似比」が解れば、図形の「線分 (辺や対角線)の長さ」が求められるし、 「相似」は、何やら図形のあらゆるデータを求めるのに役立ちそうですね! よって、相似かどうか分からない場合、「相2つの図形は相似になっており AB:CD=6:9=2:3より 相似比は2:3だと分かります。 つまり、他の辺の比も2:3になるので AE:DE=BE:CE=2:3 とわかります。 このAE:DE=2:3という中学3年数学の解説 » 図形・相似 拡大、縮小の関係を相似といいます。 三角形が相似かどうか、という相似条件の暗記と、 その証明も含みます。 ここも慣れが重要です。 入試直前期にはじめて



相似とは 記号や性質 三角形の相似条件 証明問題も解説 受験辞典




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
日本大百科全書(ニッポニカ) 相似(数学)の用語解説 一つの図形を一定点を中心として一定の比に拡大あるいは縮小してできる図形と、初めの図形とは相似の位置にあるといい、その定点を相似 第5章 図形と相似 Topic 1 拡大縮小の意味 P118 Subtopic 1 Text Text Pictures Pictures P118 Subtopic 2 ruidai ruidai2 17 Topic 2 三角形の相似条件 Reidai Reidai P1 例題5 例題6,72つの図形は相似だということが分かります。 2組の角がそれぞれ等しい これが一番単純でわかりやすいです。 2つ角の大きさが等しいと確認できれば それで相似であることが分かります。 このよう




中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく



2
第5章 図形と相似 右図の ABCで、点Aからひいた線分と辺BCとの交点を点Pとし、点Pからひいた線分と辺ACとの交点を点Qとする。 AB=16cm、BC=18cm、BP=8cm、∠ABC=∠QPC のとき以下 相似とは、 形はまったく同じで、大きさの違う図形同士の関係 です。 つまり、相似な図形同士は 拡大・縮小の関係 にあるといえますね。 また、裏返した図形においても相似は成り立ちさて、ある種の図形がすべて相似だという例が他にあるかと考えると、直線だ。つまり放物線は直線と同じくらい基本的な図形なのである。 〜 考えるための数学問題集 〜 わかれば瞬殺、答えを見




中学3年数学練習問題 図形と相似の定期テスト対策問題
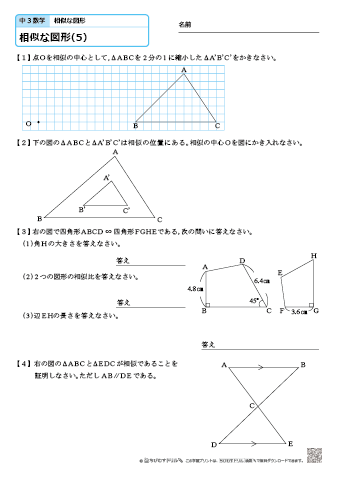



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
中3数学図形と相似相似な図形と証明(1~9)のプリント集です。 相似な図形 三角形の相似条件① 三角形の相似条件② 相似条件と証明① 相似条件と証明② 相似条件と証明③ 相Try IT(トライイット)の図形と相似の映像授業一覧ページです。 図形と相似の勉強・勉強法がわからない人はわからない単元を選んで映像授業をご覧ください。 相似の文章題(かげの長さ) 拡大図・縮図の作図 三角形の相似条件1(3辺の比) 図形と相似 中3数学で学ぶ「図形と相似」のテストによ 相似比とは、 相似な図形の対応する辺の長さの比 のことを言います。 つまり、図形を何倍拡大もしくは縮小することによって つの図形が一致するか、を示す比です。 相似比を求める



1




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
合同な図形は相似な図形でもあるので、この2つの図形は相似となる。 相似比 相似な図形で、対応する線分の長さの比を相似比(そうじひ)といいます。 三角形の相似条件 2年生では三角形が合同 相似条件1 「3つの辺の比が等しい」 「3つの辺の比」 がすべて等しいとき、2つの三角形は相似って言えるんだ。 たとえば、2つの ABCと DEFを想像してみて。 AB = 6 cm BC = 8 cm上の図で、 辺DEと辺BCが平行ならば、三角形ADEと三角形ABCは相似 です。 こちらも、必ず平行であることを確認してください。 それと、チョウチョの形と比べて、三角形の位置関係を間違えや



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ




無料 中3数学 基本問題 解答プリント 図形の相似2 相似条件と証明
相似の意味 形は同じだが、大きさが違う2つ (以上)の図形を「相似 (そうじ)の関係にある」という 合同との違い 「合同」は形だけでなく大きさも同じ2つ (以上)の図形の関係を言う 練習




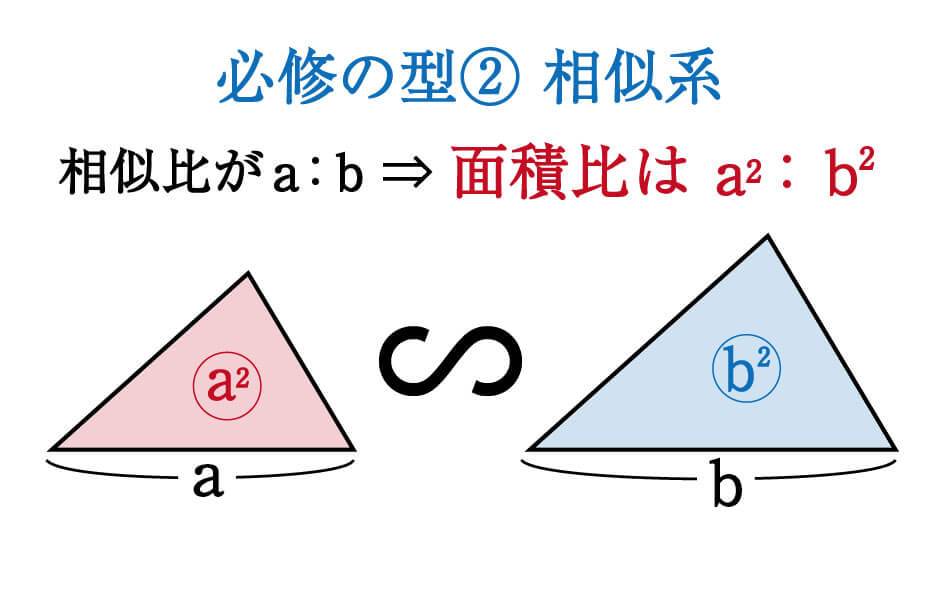
3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく
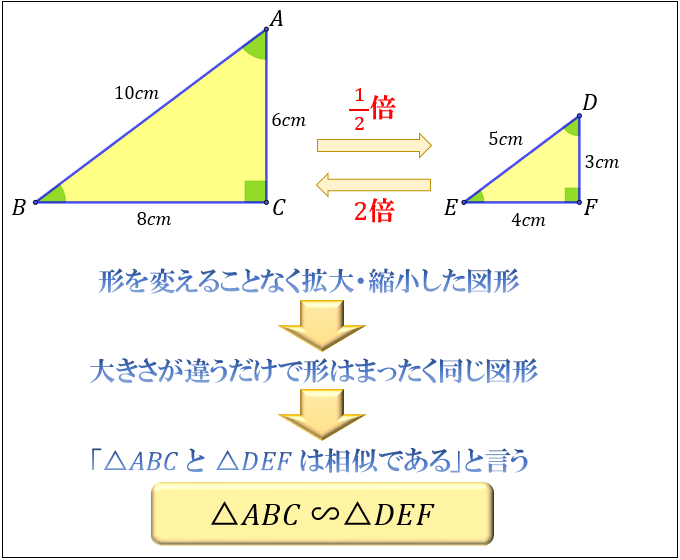



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ




中3数学 相似の基本性質をわかりやすく問題解説 数スタ




世界一わかりやすい数学問題集中3 5章 図形と相似
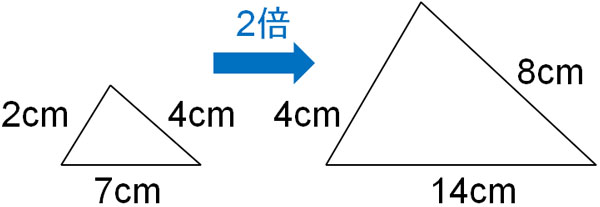



中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 Hatsudy 総合学習サイト




相似な図形 はこれでカンペキ 相似な図形のかき方8種類 算数を究める




中3数学 相似と線分比1 平行四辺形 Youtube
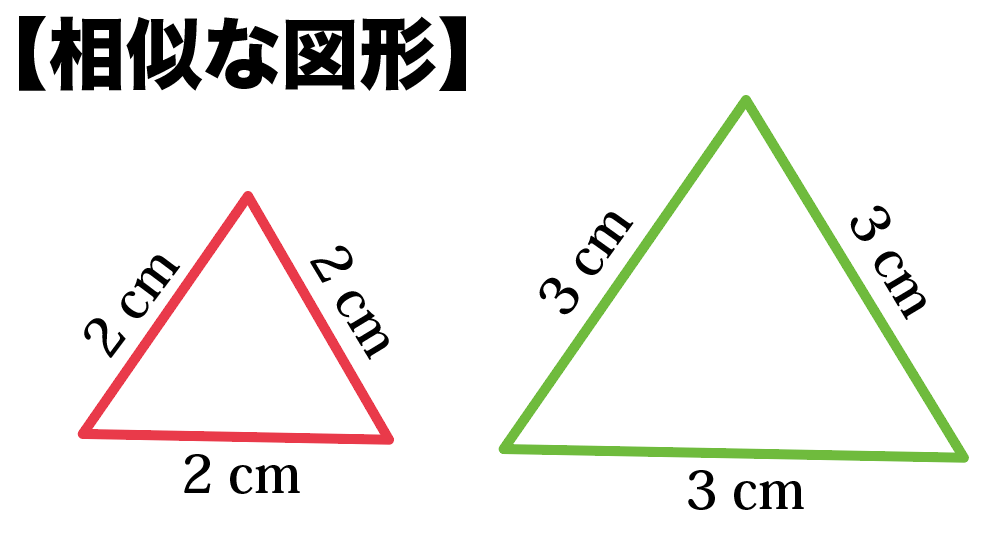



知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく
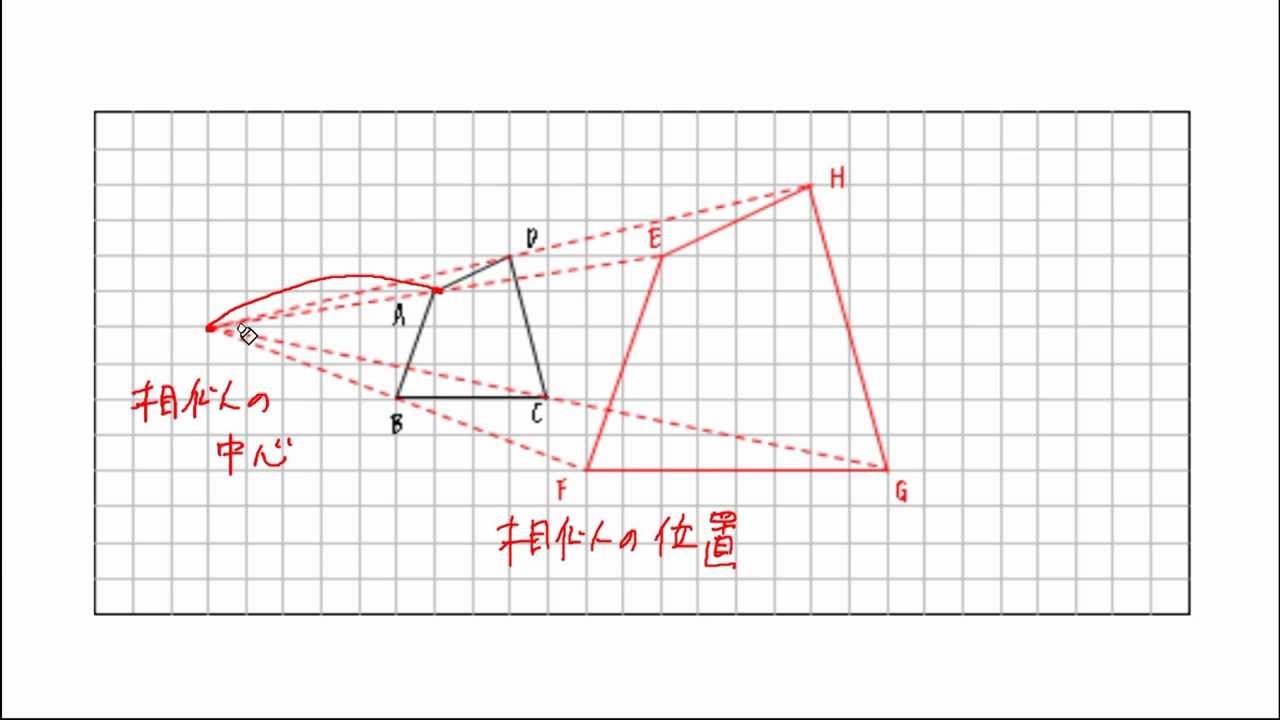



相似の中心と作図 Youtube



Tossランド 相似な図形



相似な図形の作図 Geogebra



相似とは 記号や性質 三角形の相似条件 証明問題も解説 受験辞典



Math 空間図形と相似 面積比 体積比 発展問題 働きアリ



相似な図形の特徴 Geogebra



図形の相似 規則集3 中学から数学だいすき




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題
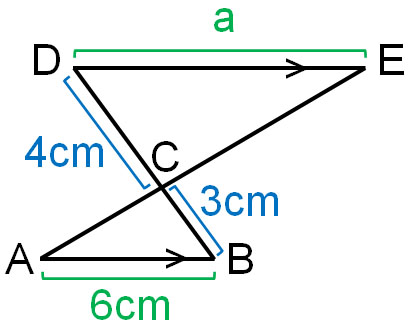



中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 Hatsudy 総合学習サイト
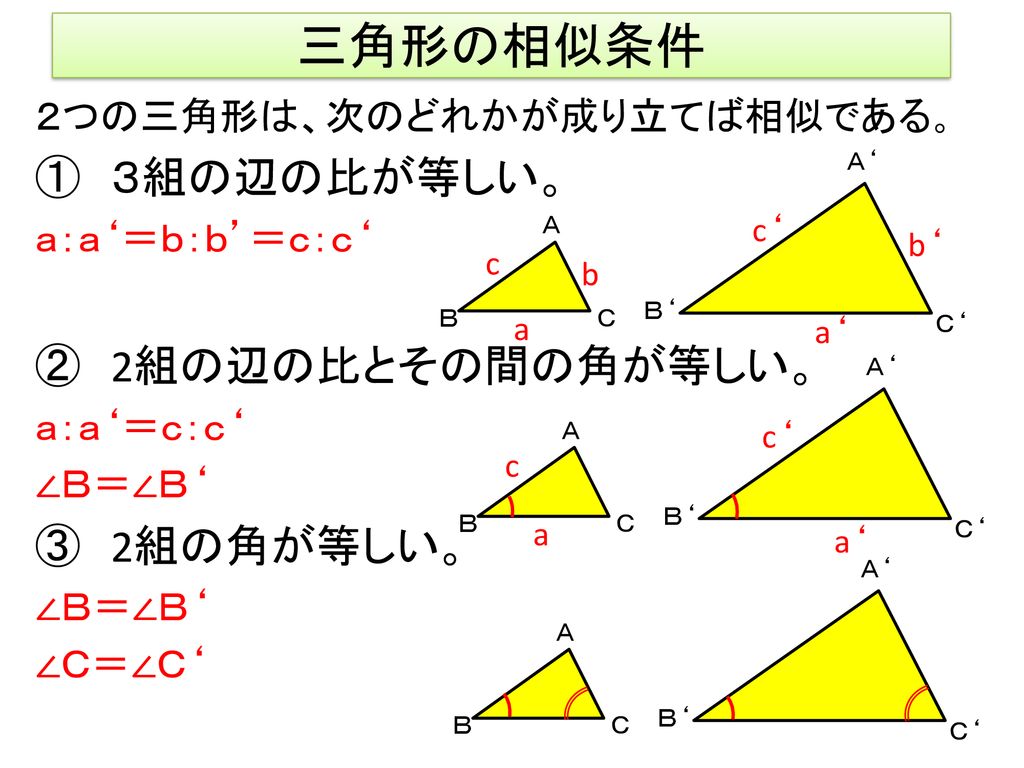



本時のねらい 図形の中から相似な三角形を見出し 相似条件を用いて証明することができる Ppt Download
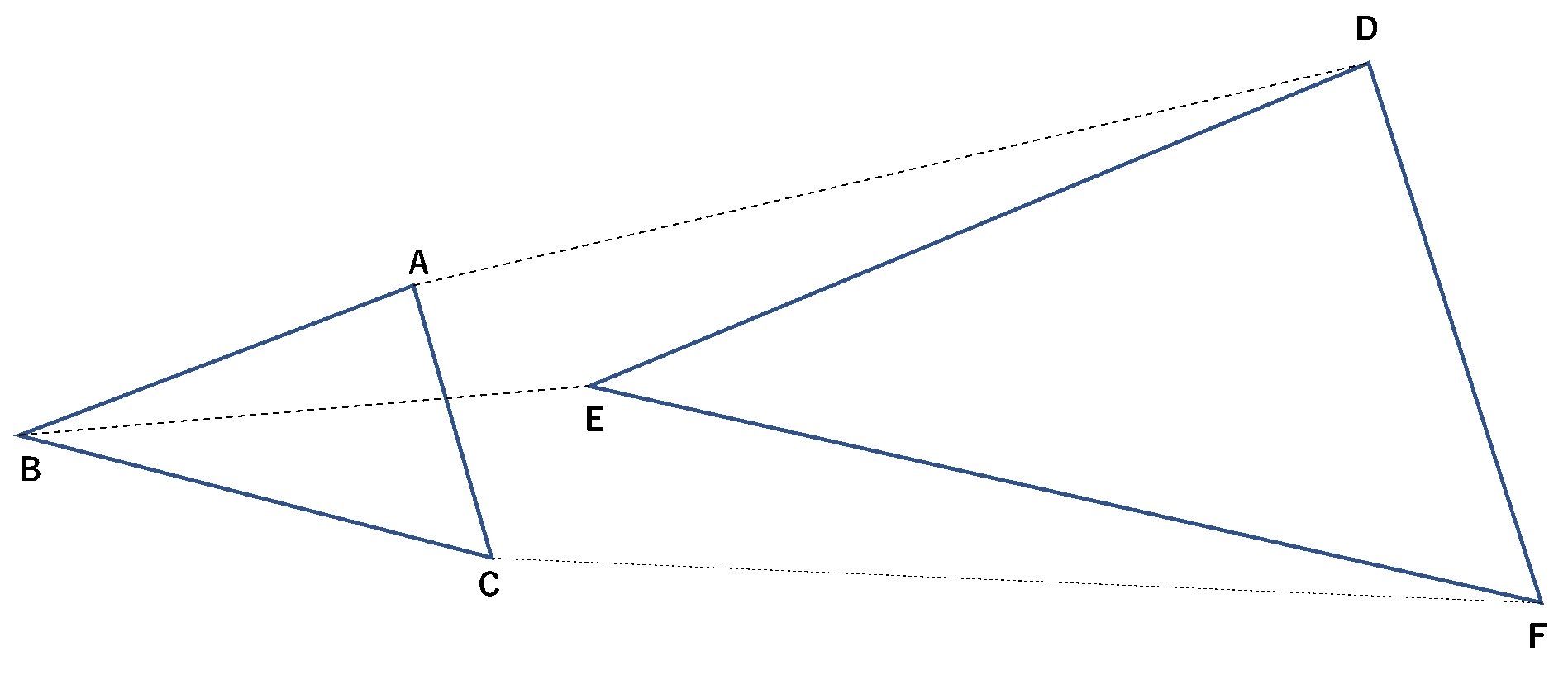



相似な図形とは 算数からやさしく解説 数学 統計教室の和から株式会社




中3数学 図形と相似27 相似な図形の面積比 星組の中学数学講座
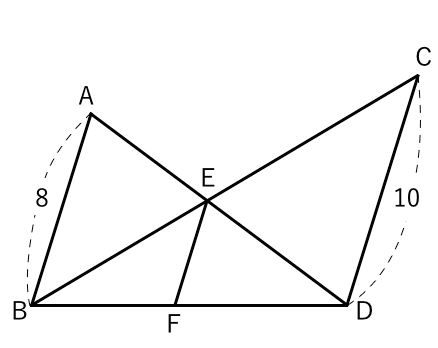



相似な図形 ピンポイント計算式 苦手な数学を簡単に




世界一わかりやすい数学問題集中3 5章 図形と相似
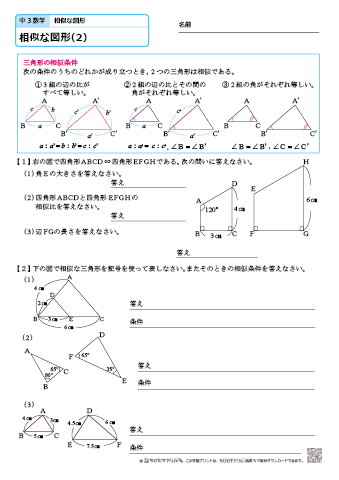



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
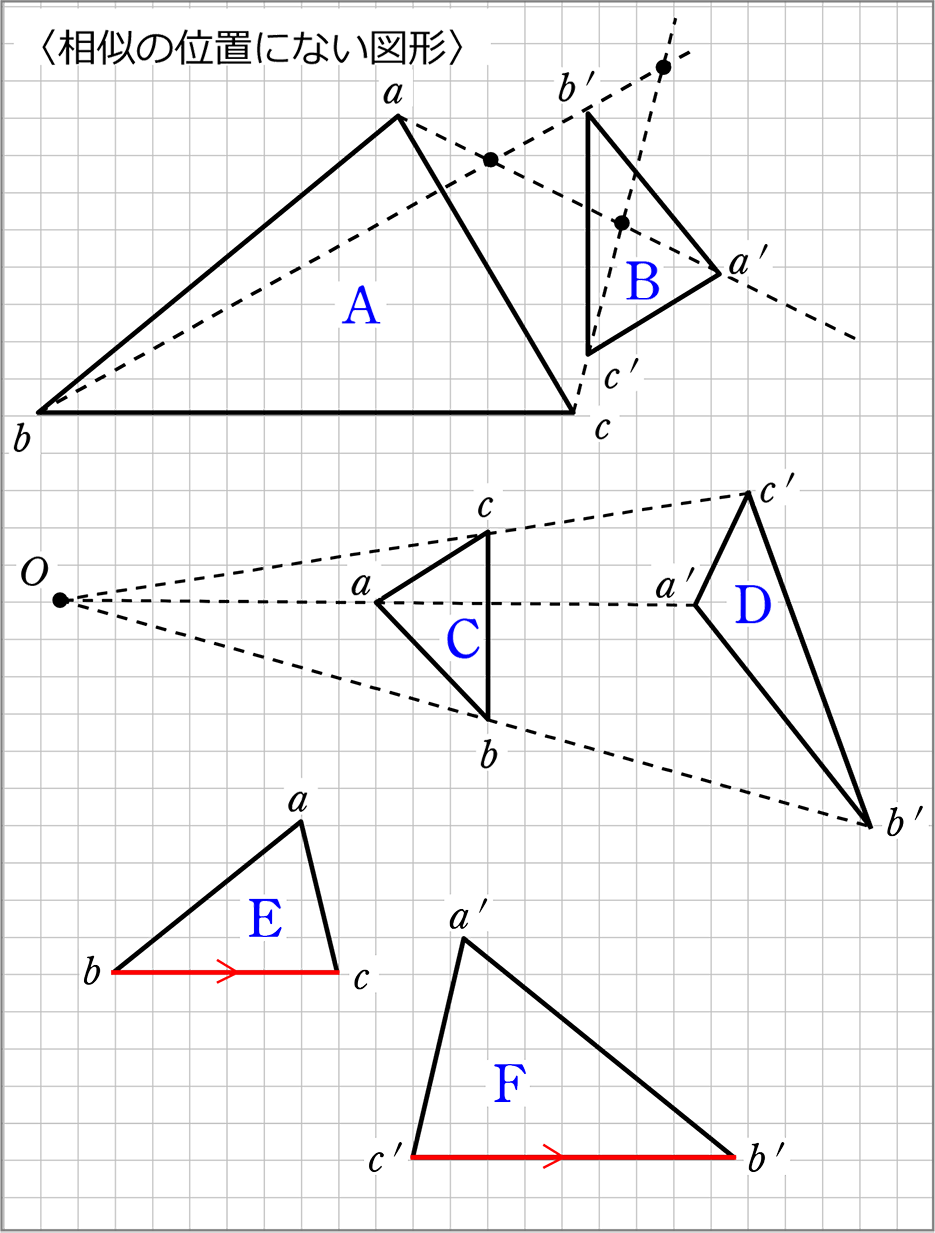



中学数学 図形の相似



2
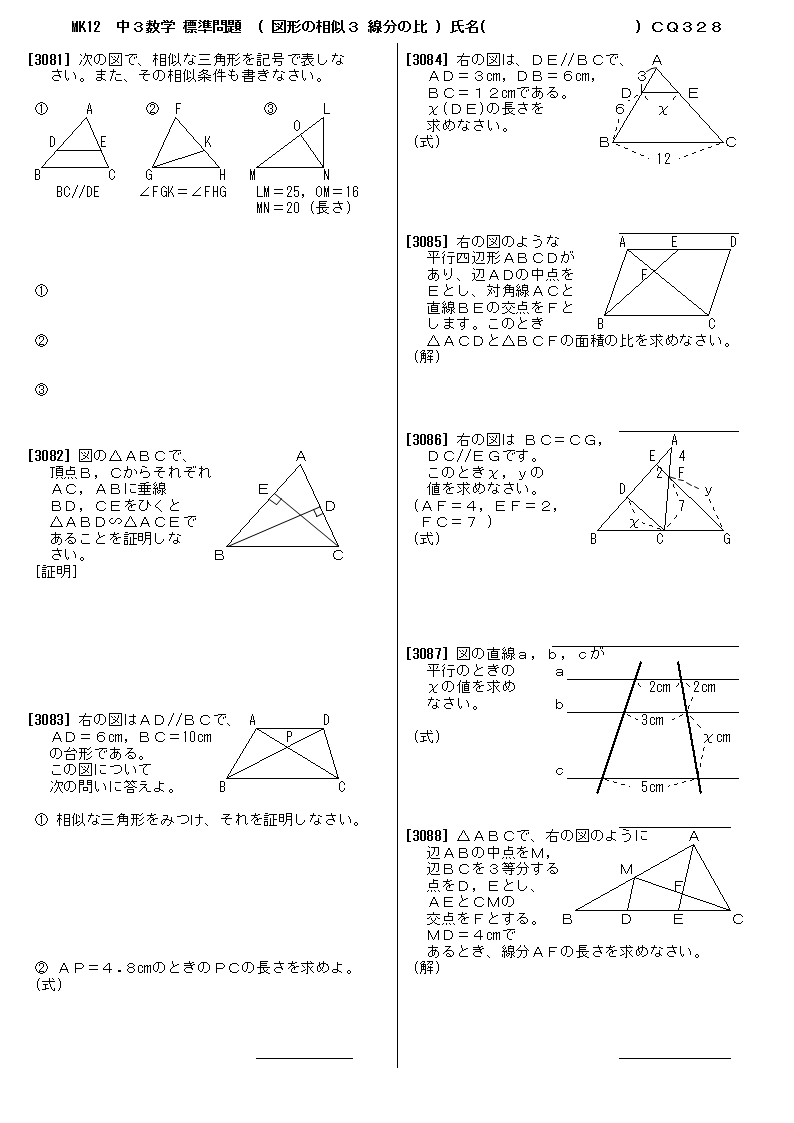



無料 中3数学 標準問題 問題プリント 328 図形の相似3 線分の比




図形と相似 Qikeru 学びを楽しくわかりやすく
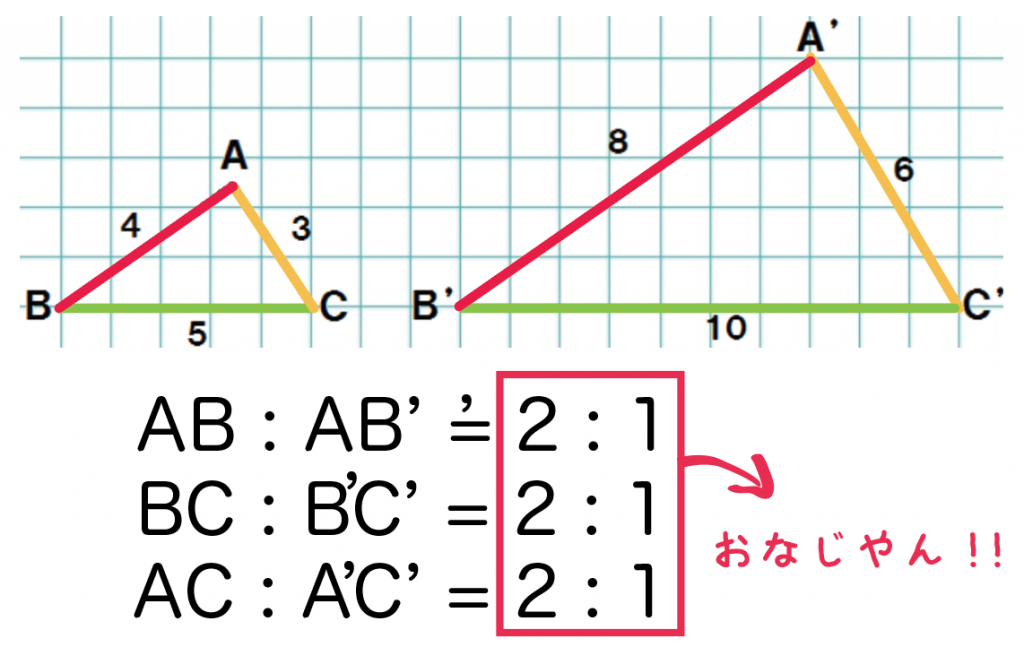



中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく



2
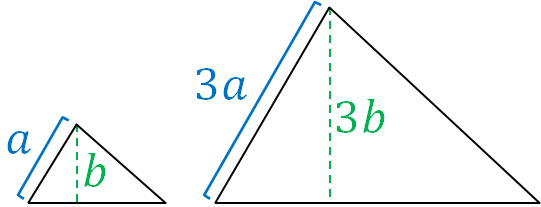



中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 Hatsudy 総合学習サイト




世界一わかりやすい数学問題集中3 5章 図形と相似




無料 中3数学 標準問題 解答プリント 328 図形の相似3 線分の比
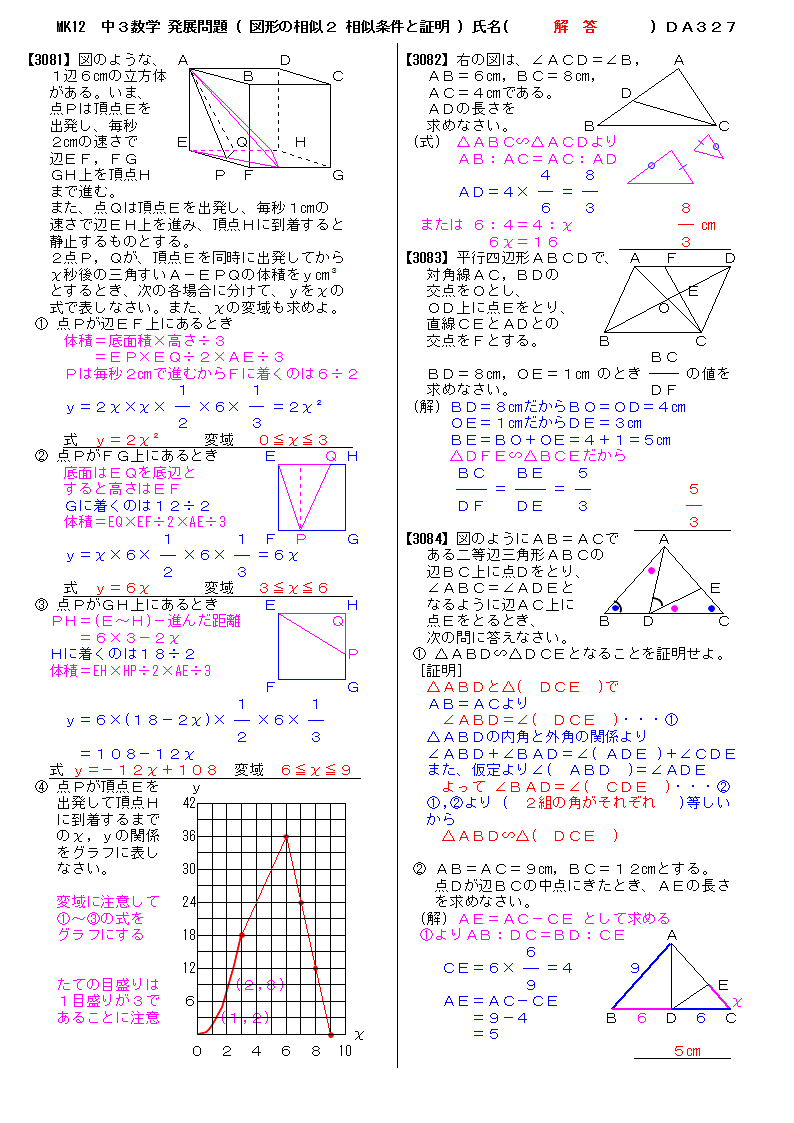



無料 中3数学 発展 応用問題 解答プリント 327 図形の相似2 相似条件と証明



相似とは 記号や性質 三角形の相似条件 証明問題も解説 受験辞典
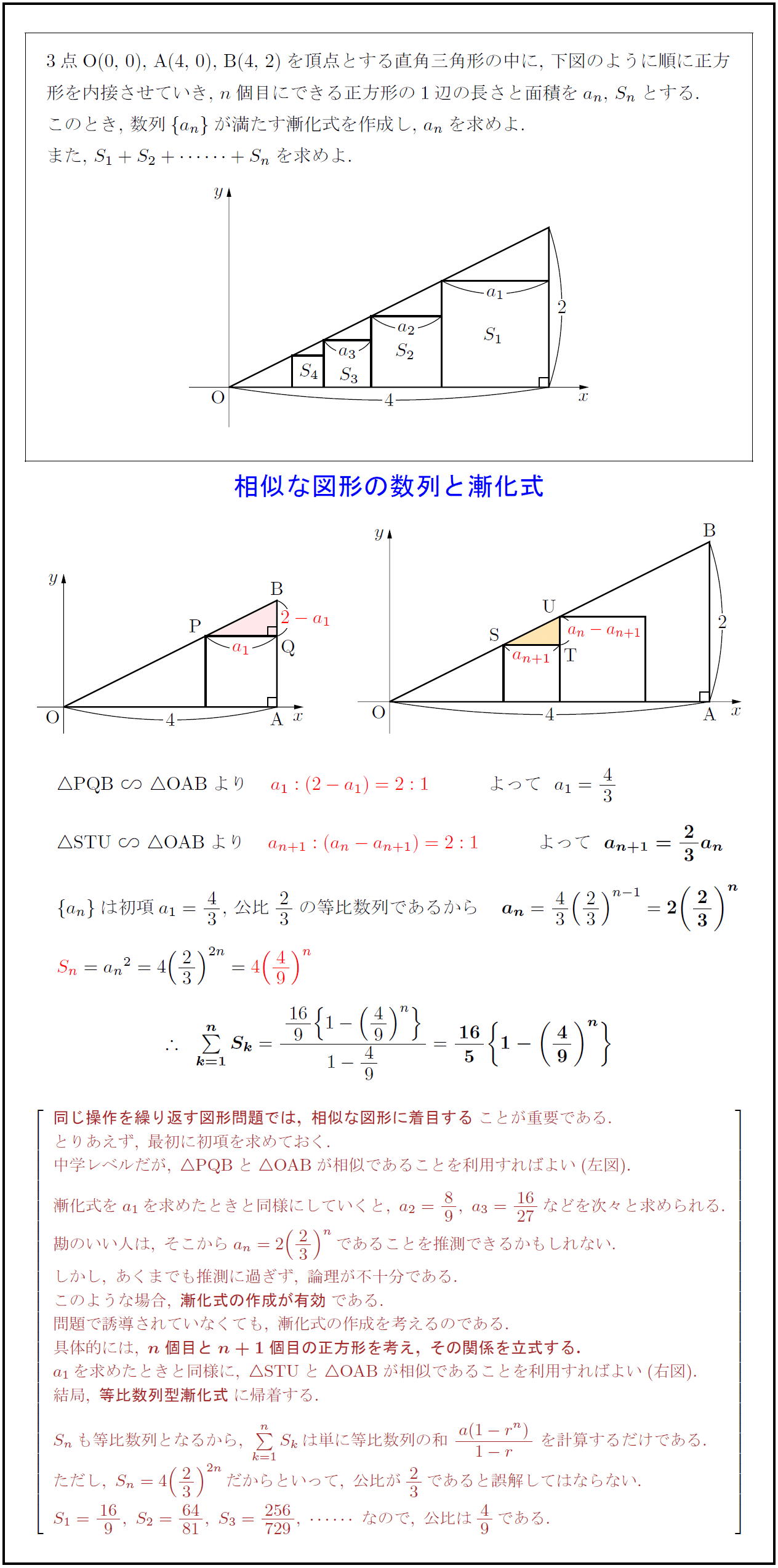



高校数学b 相似な図形の数列と漸化式 受験の月
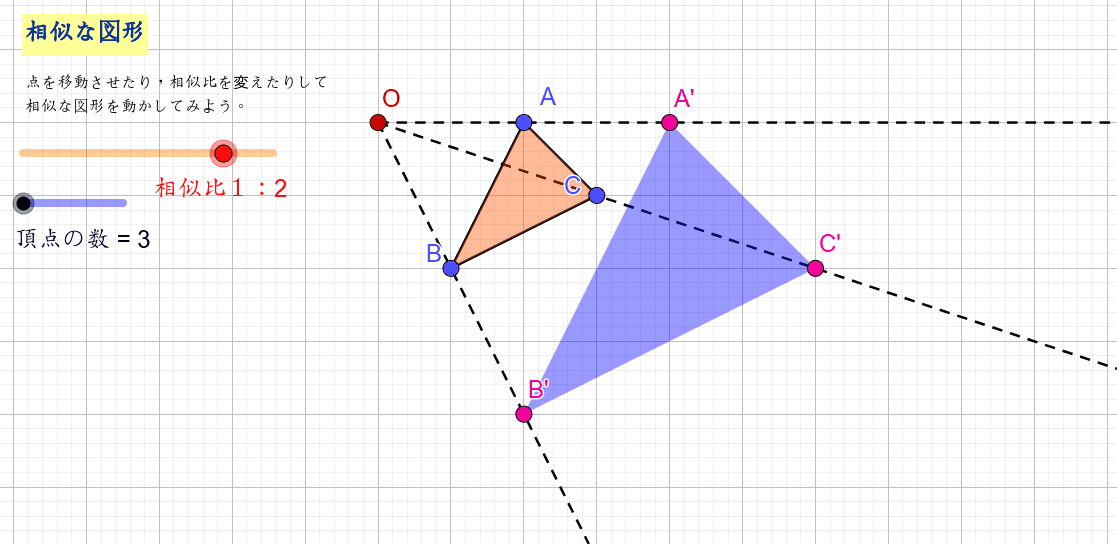



相似の位置 Geogebra
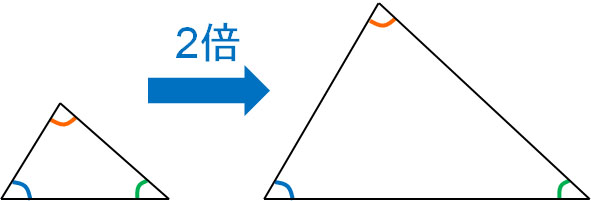



中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 Hatsudy 総合学習サイト
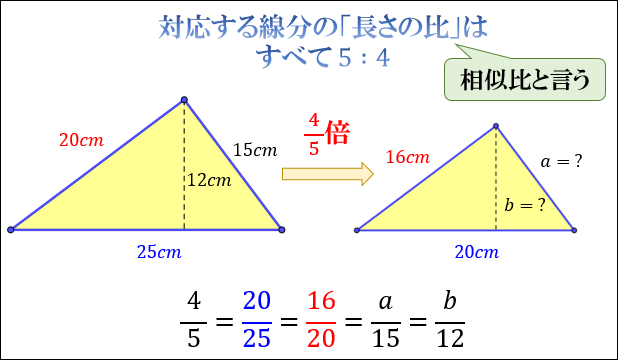



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ
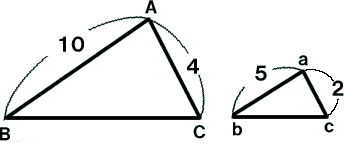



相似比
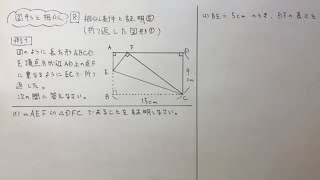



中3数学 図形と相似8 相似条件と証明 折り返した図形 星組の中学数学講座




中学三年相似な図形の範囲です の問題なのですが 何故 相似比が3 2 数学 教えて Goo




相似な図形 Ict教材eboard イーボード



Studydoctor相似な図形や中心の作図 中3数学 Studydoctor
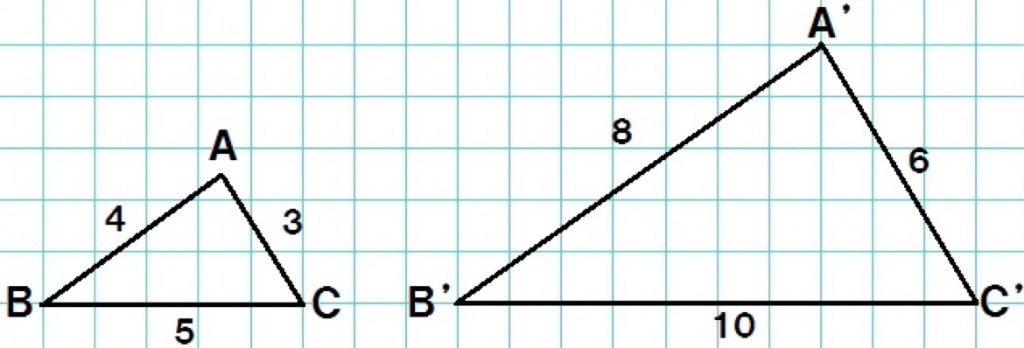



中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく




相似な図形 Ict教材eboard イーボード
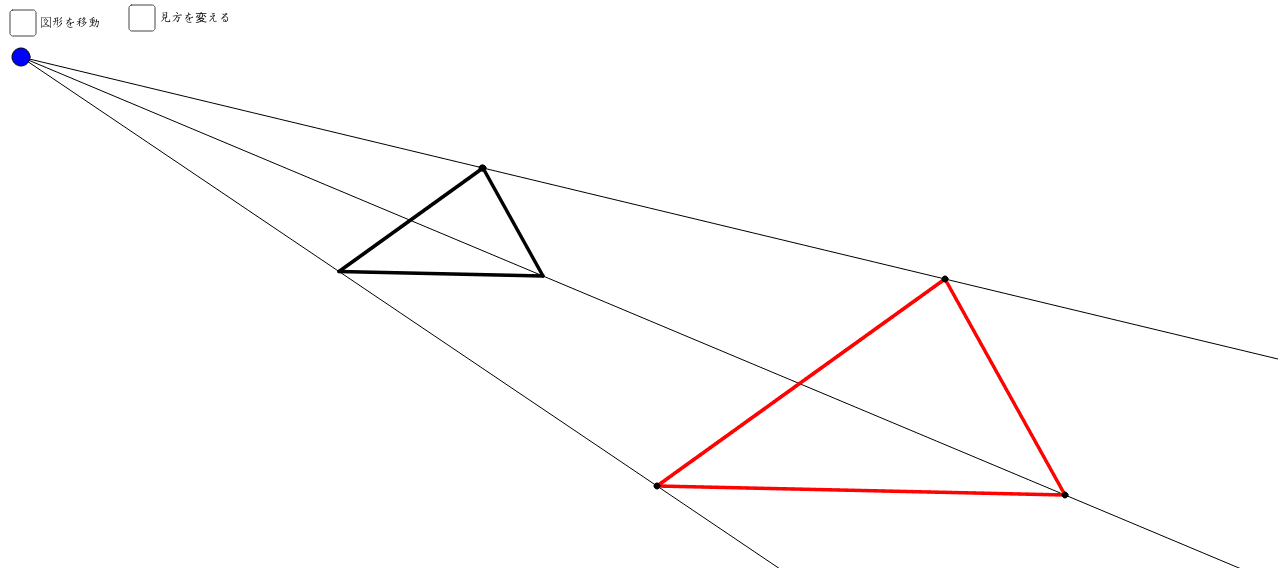



相似な図形の特徴 Geogebra




相似な図形 Ict教材eboard イーボード
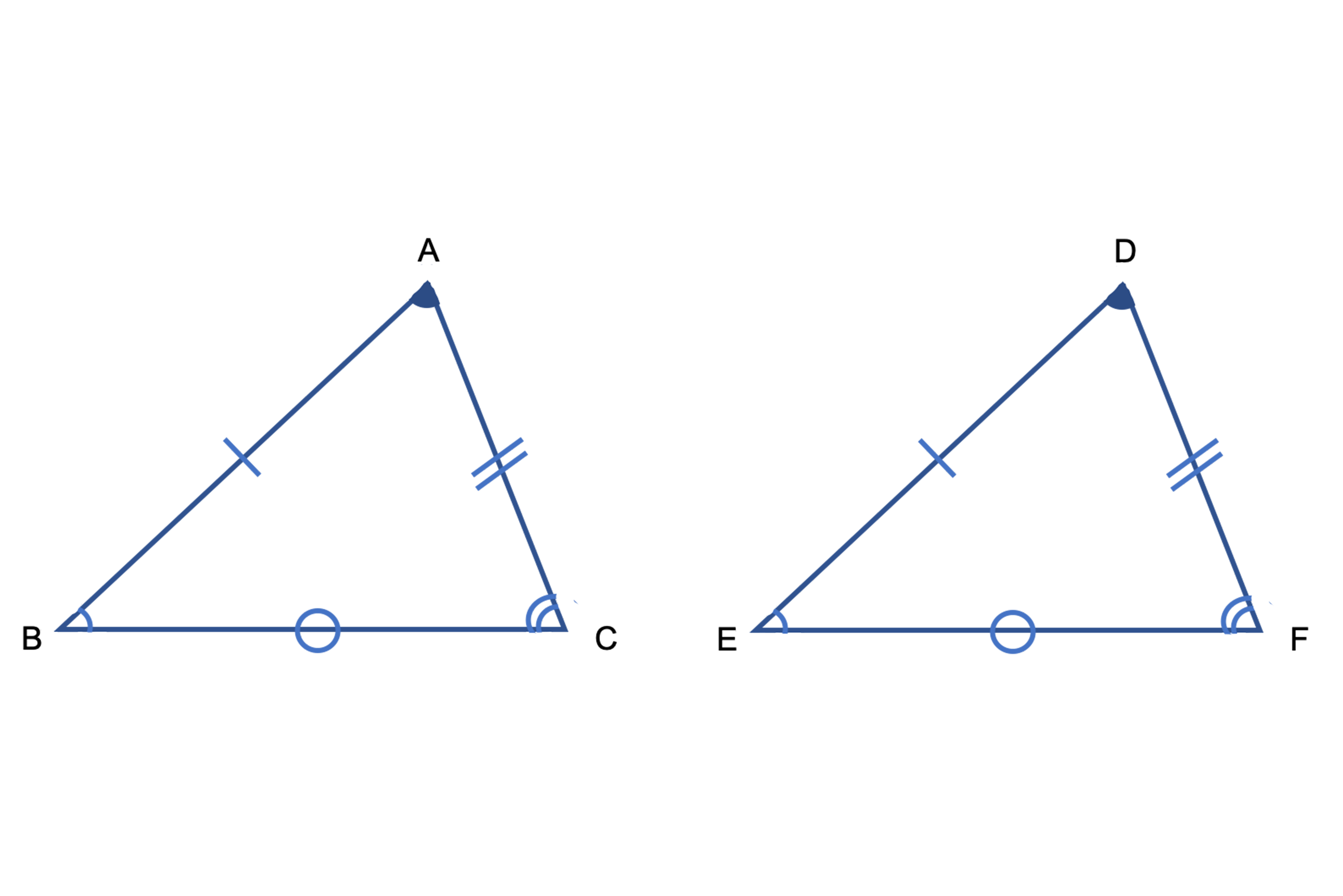



記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス
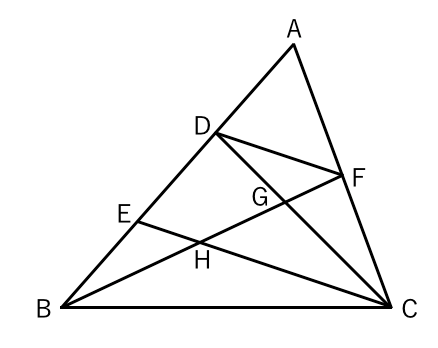



相似な図形 平行線と線分の比 よく出る系 苦手な数学を簡単に
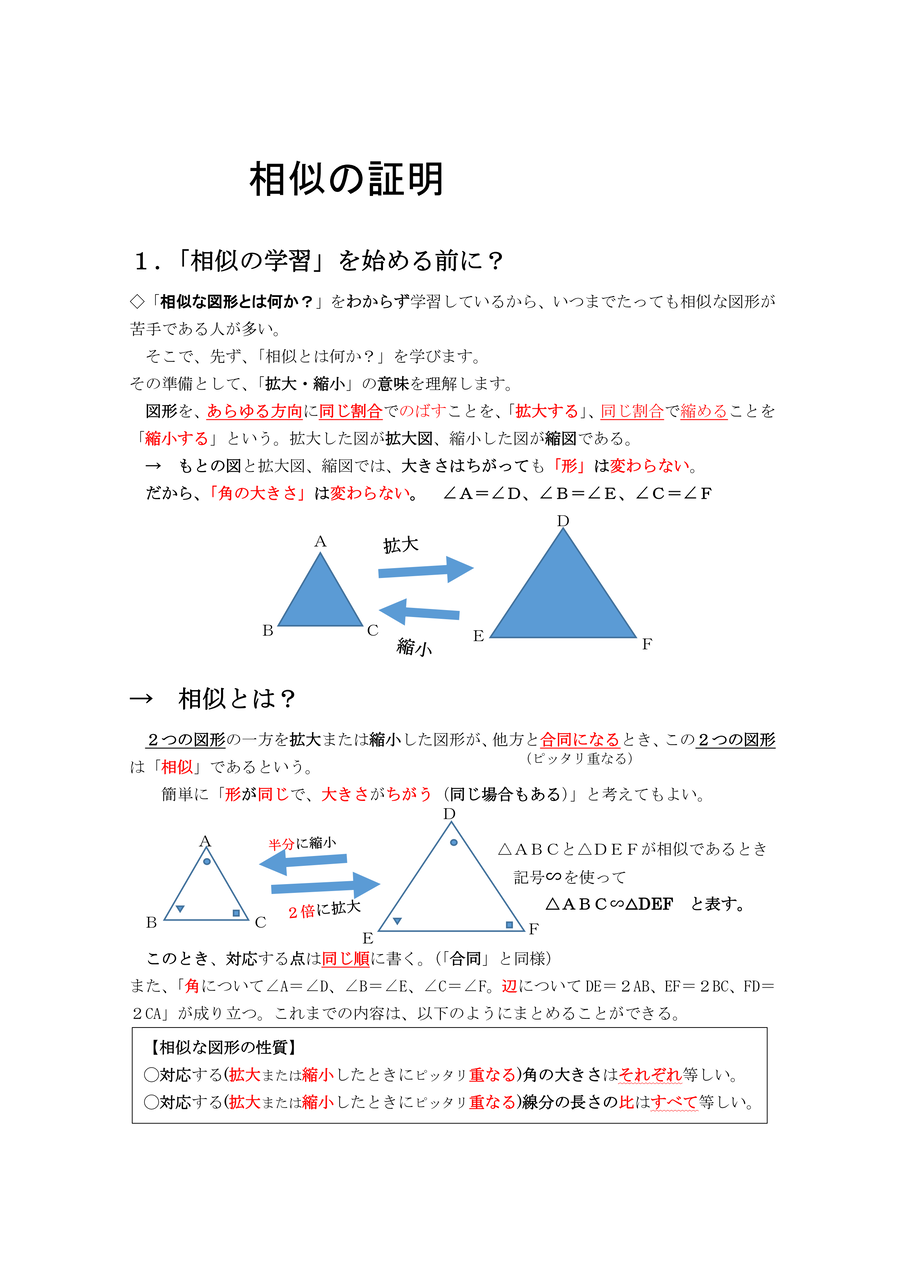



中学校数学 証明のコツ 相似
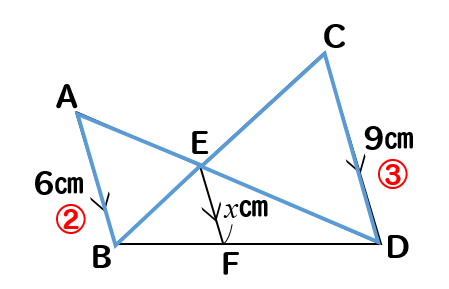



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




図形と相似 の問題のわからないを5分で解決 映像授業のtry It トライイット




補助線を引いて考える相似の問題 相似な図形 中学生からの勉強質問 数学 進研ゼミ中学講座
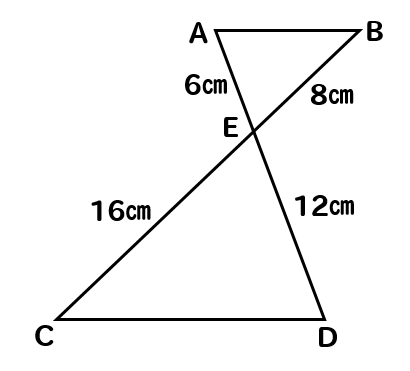



中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ




世界一わかりやすい数学問題集中3 5章 図形と相似




図形の相似 Wikipedia



相似とは 記号や性質 三角形の相似条件 証明問題も解説 受験辞典




Math 相似 相似の難問を ちょうちょ と おむすび で簡単に解く 1 働きアリ




中3数学 図形と相似31 相似な図形の面積比 星組の中学数学講座
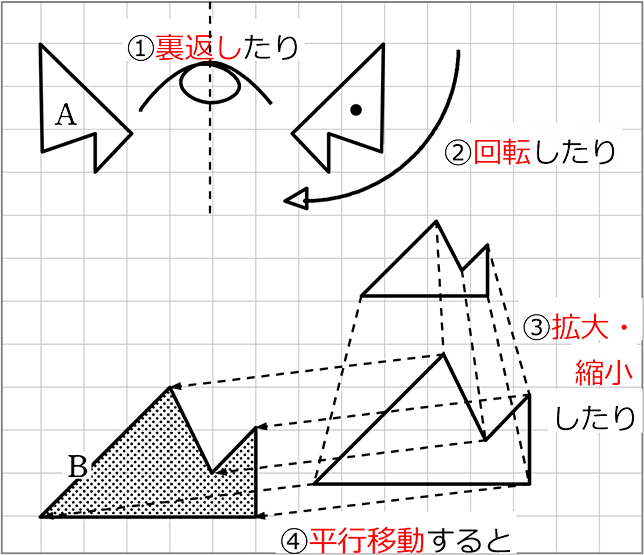



中学数学 図形の相似
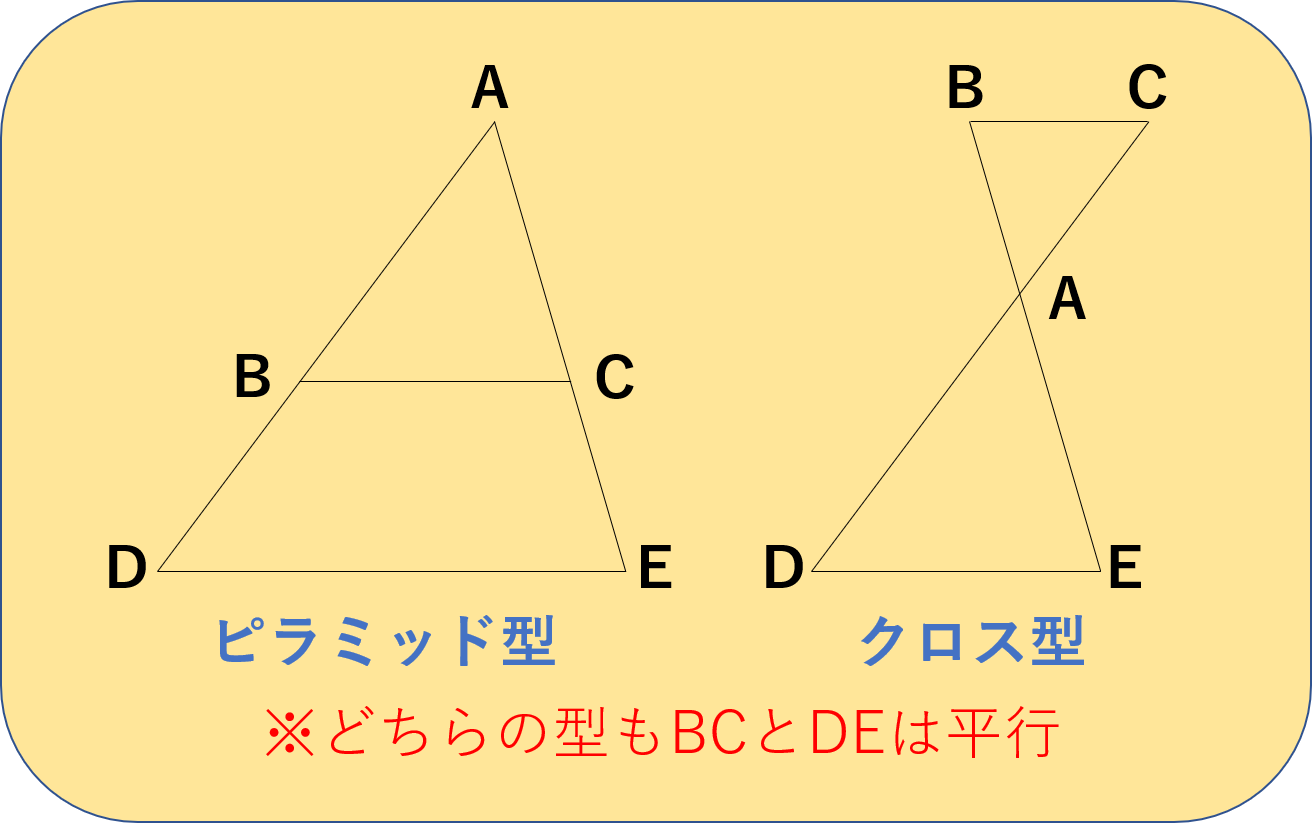



平面図形と比 相似形を作ってみよう 中学受験プロ講師ブログ
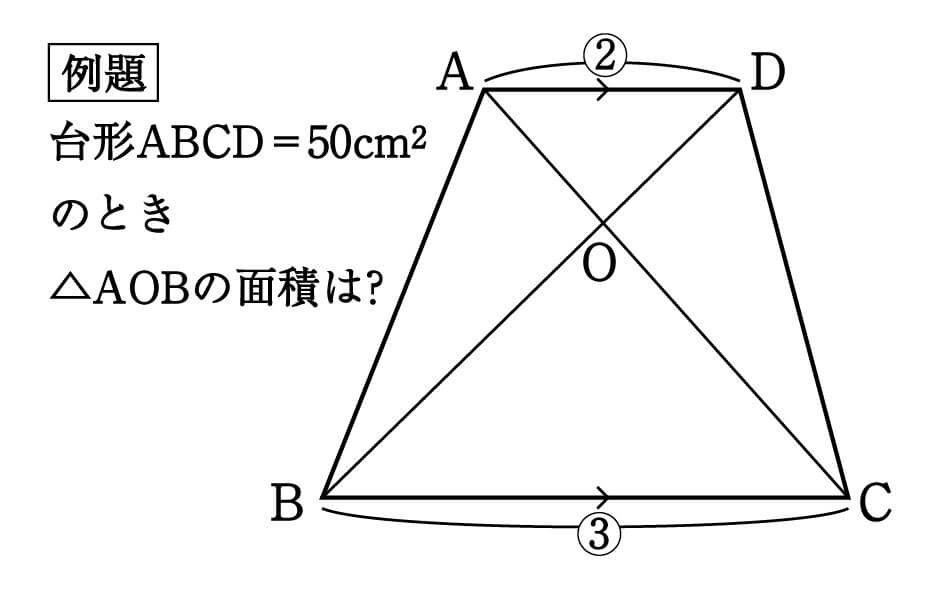



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
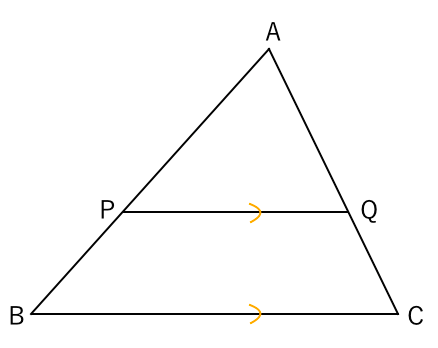



相似な図形 計算について覚えること 苦手な数学を簡単に



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生
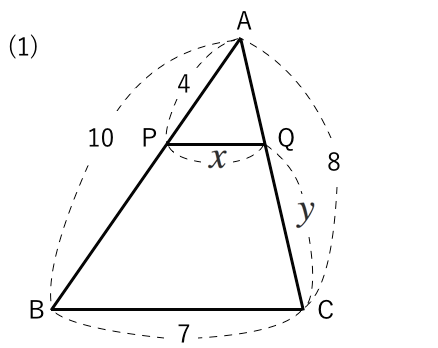



相似な図形 長さを求める 苦手な数学を簡単に



2




相似な図形 三角形の相似条件 中学数学 By となりがトトロ マナペディア
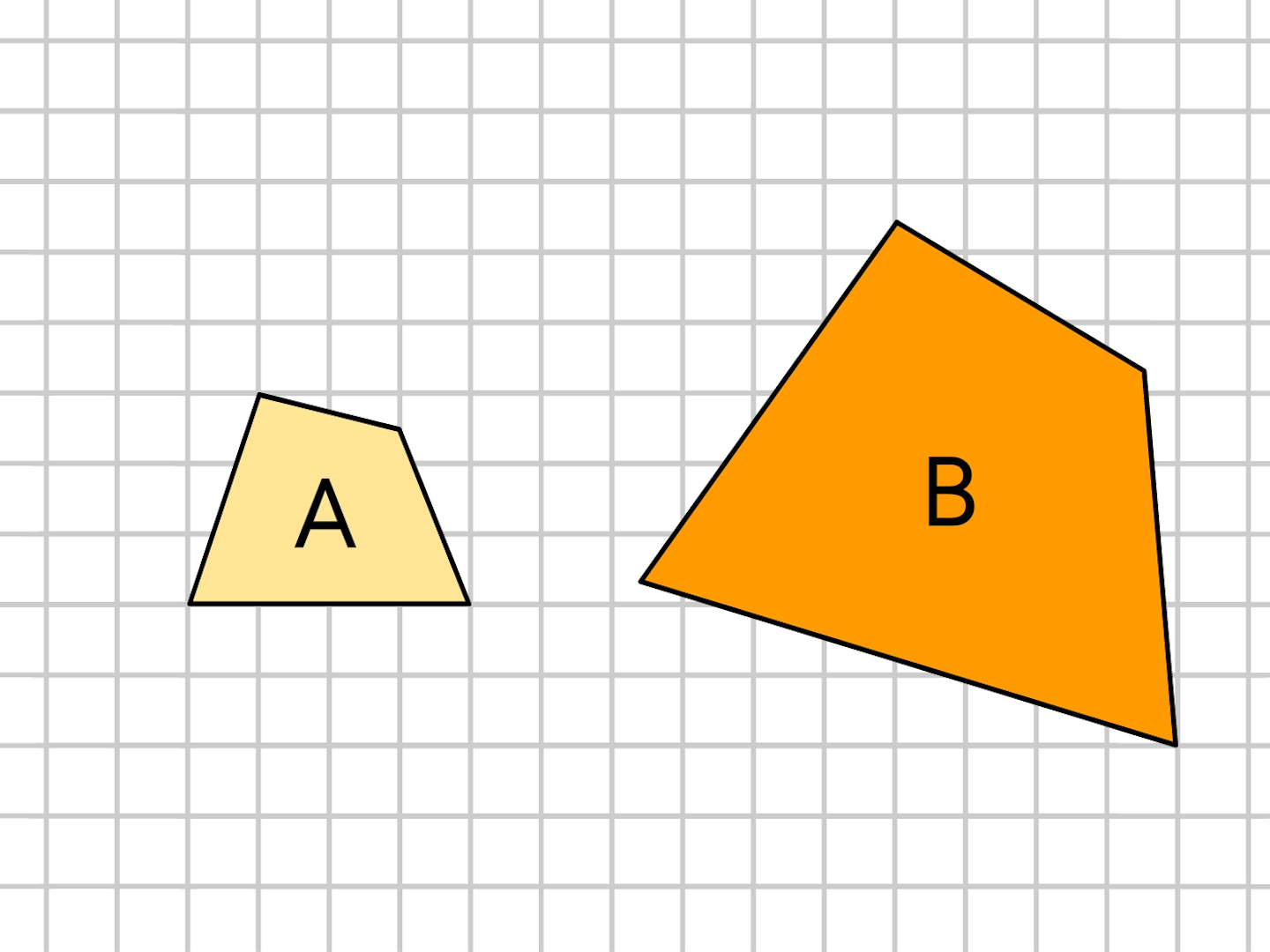



3年 相似な図形とその性質 数学イメージ動画集 大日本図書



1
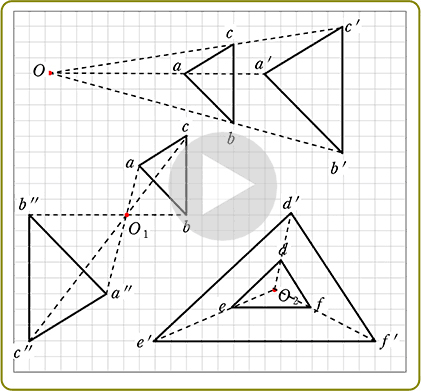



中学数学 図形の相似




スタディピア 図形 ホームメイト



相似を見つけよう 平面図形 パズル おもしろ算数問題
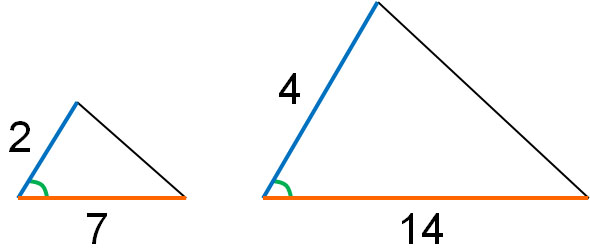



中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 Hatsudy 総合学習サイト



第5章3 三角形の相似 相似な図形の性質 The 教科書 プログラミング
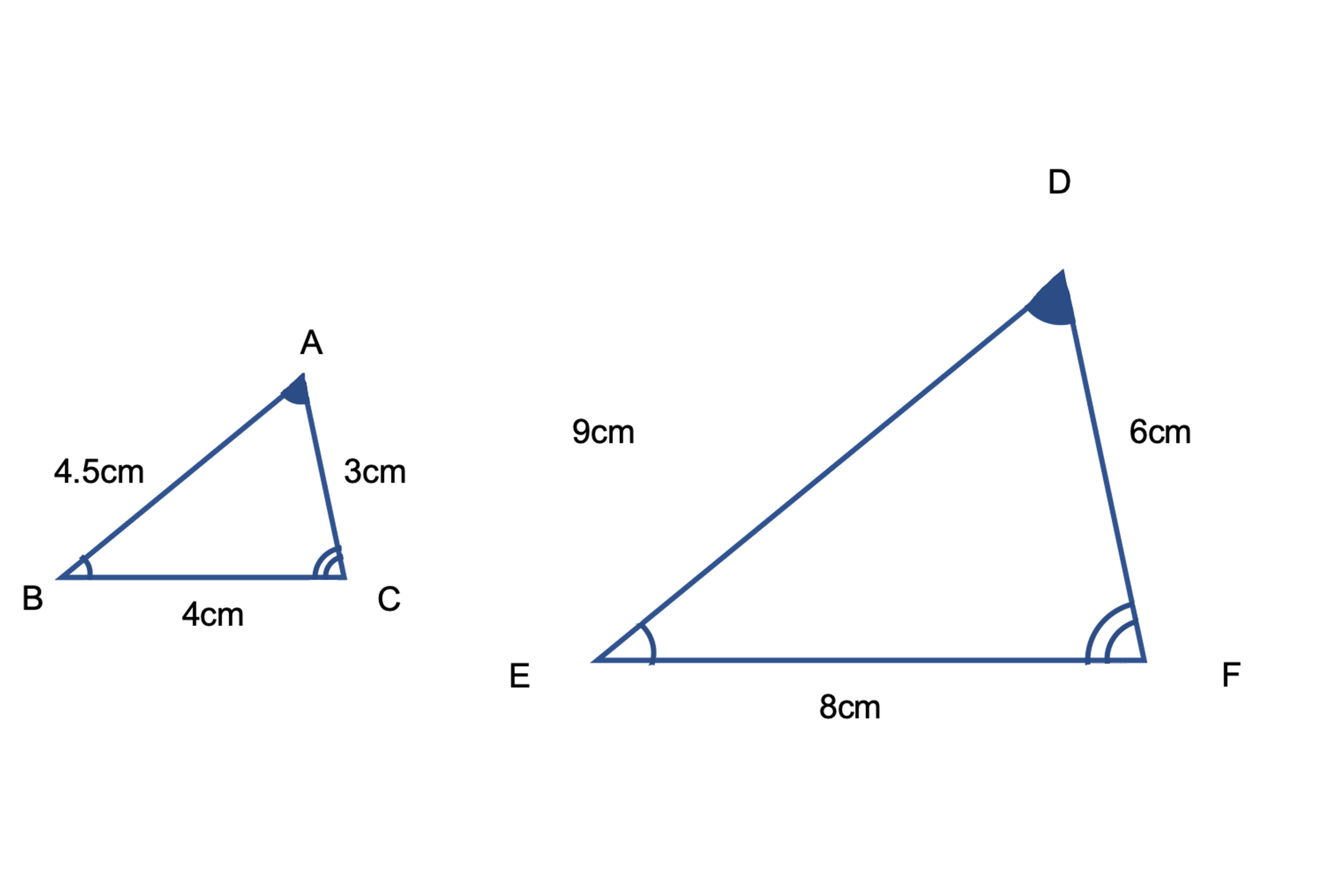



記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su




中3 相似な図形とは 基本問題にチャレンジ Youtube



2



相似 Geogebra
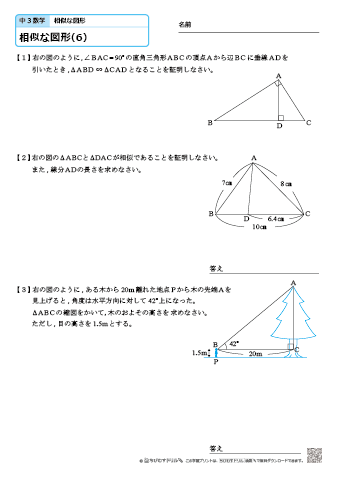



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3数学 図形と相似9 相似条件と証明 折り返しの図形 星組の中学数学講座
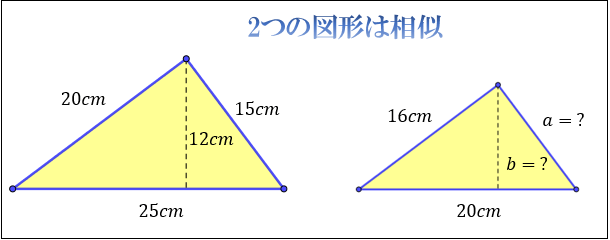



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ



相似比とは 1分でわかる意味 面積比 四角形と三角形の問題
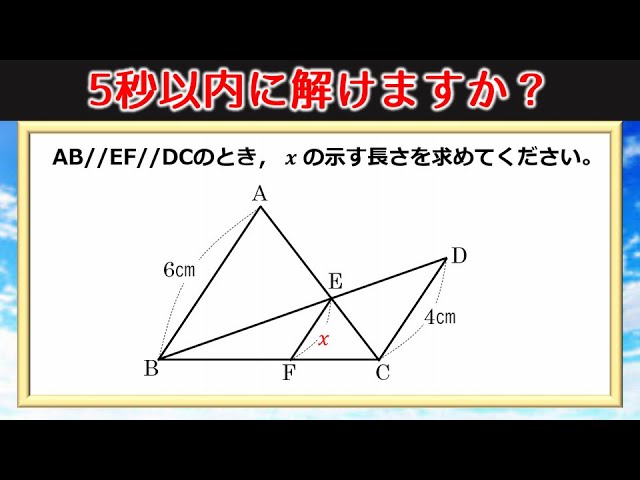



図形問題 知っている人は5秒で解ける相似の裏技 Youtube
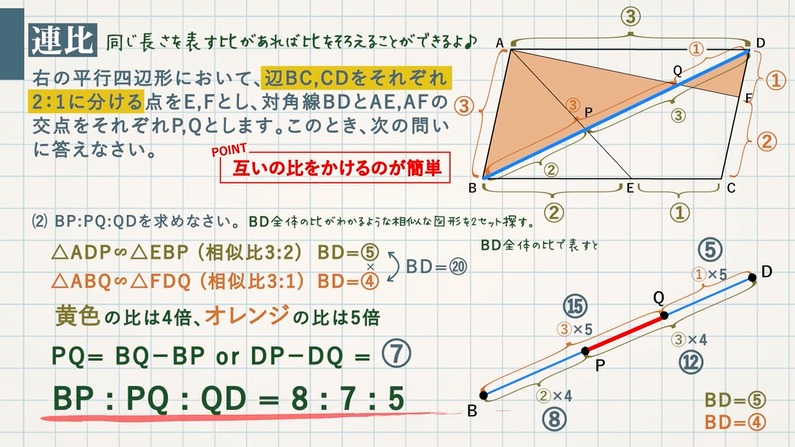



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者



0 件のコメント:
コメントを投稿